Untersuchung der Eignung des Luftqualitätsindex als Primärer Indikator für Industrielle Gewässerverschmutzung: Eine Fallstudie zu Südkoreas Han und Österreichs Donau
Jiwoo Jung
Die American International School of Vienna
(The American International School of Vienna)
jiwj07@gmail.com
PDF: https://shorturl.at/Sck1H
Zusammenfassung

Weltweit leiden Milliarden von Menschen weiterhin unter der Verunreinigung von Gewässern, deren Ausmaß und Schwere der Auswirkungen immer weiter zunehmen. Doch verglichen mit den Hunderttausenden von Flüssen weltweit erscheint der Umfang der Studien zur Analyse der Wasserqualität von Flüssen verschwindend gering. Da die Industrialisierung weiterhin vor allem das Oberflächenwasser von Flüssen kontaminiert, wird die Untersuchung von Gewässern zunehmend dringlich. Diese Forschung vergleicht und bewertet die industrielle Verschmutzung des südkoreanischen Han-Flusses und der österreichischen Donau, indem unabhängig erhobene Daten zu Wasserparametern wie gelöstem Sauerstoff (DO), pH und Gesamtgehalt gelöster Stoffe (TDS) interpretiert sowie vorhandene Informationen zu beiden Flüssen, sowohl quantitativer als auch qualitativer Art, ausgewertet werden. Öffentliche Daten zur Bevölkerungsdichte (HPD) und zum Luftqualitätsindex (AQI) wurden genutzt. Unter Verwendung des Kumulativen Luftqualitätsindex (CAI) als AQI für beide Flüsse zeigten alle Daten eine sich verschärfende industrielle Verschmutzung im Han, während die Donau eine beherrschbare Kontaminationsstufe aufwies. Die Daten wurden außerdem zur Erstellung von Matrizen der Pearson-Korrelationskoeffizienten verwendet, wobei die Matrix, die die erhobenen Daten kumulativ bewertete, starke Korrelationen zwischen allen Paaren der untersuchten Parameter zeigte und damit die Bewertung der industriellen Verschmutzung beider Flüsse weiter untermauerte. Die Daten wurden zum Trainieren und Testen von 185 Kombinationen überwachter Machine-Learning-Modelle in Python verwendet, wobei verschiedene Ebenen der Merkmalsauswahl zum Einsatz kamen. Schließlich wurden Daten aus öffentlichen Datenbanken zusammengeführt, um lineare Modelle, nichtlineare Support-Vector-Regressionen (SVR) und Modell-Ensembles zu erstellen, unter Anwendung k-facher Kreuzvalidierung und unter Unterscheidung zwischen Methoden der Merkmalsauswahl und Techniken der Dimensionsreduktion, um eine hohe Genauigkeit sicherzustellen.
Schlüsselwörter: Umweltwissenschaften, Ökologie, Flusshydrologie, industrielle Verschmutzung, maschinelles Lernen
1. Einführung
The rise in global pollution poses significant risks to both ecosystems and modern society. The contamination of rivers complicates the current cultural, economic, and political dynamics among human populations. Rivers foster unique biodiversity patterns that help mitigate the detrimental effects of human activities (Blanchet et al., 2020). Moreover, while rivers facilitate hydrologic, geomorphic, and ecological connectivity, they also play a crucial role in transferring organisms and sustaining biodiversity through the cycling of water. As global civilization increasingly urbanizes, the social connections among human populations become even more pronounced (Kondolf & Pinto, 2016). Additionally, river and environmental flows serve as a means to mitigate the impacts of anthropogenic activities, directly linking cultural values and lifestyles of communities while also protecting and restoring aquatic ecosystems (Anderson et al., 2019).
Water pollution is the contamination of water bodies, including rivers, lakes, oceans, groundwater, and even aquifers, by harmful substances, critically affecting the human population by placing human health, ecosystem, and the availability of water at risk (Mohamed, 2024). Affecting river flows as well, numerous aquatic systems around the world experience degradation as environmental flows become compromised despite its growing importance. Such degradation raises the urgency to maintain the water quality of rivers and environmental flows (Anderson et al., 2019). Since water is a fundamental aspect of the environment that provides important benefits for the human population, the management of water quality is essential: “Water is life without pollution, but death when it is polluted” (Igwe et al., 2017). The immediate call to action presents a crucial need to reduce the harm caused by water pollution to the ecosystem and human health. Among the two million people dying each year due to diarrhoeal illnesses, substandard sanitation of drinking water has led to approximately 90% of such deaths (Lin et al., 2022).
To discuss the pollutants of river pollution, anthropogenic activities such as agriculture appear to bring contamination and subsequent pollution to our varied ecosystems (Bashir et al., 2020). 38% of the streams extending across European nations are “significantly under agricultural pressure”; in the United States, agriculture is one of the primary sources of pollution within rivers and wetlands; agriculture has resulted in severe surface-water pollution and groundwater pollution of Chinese rivers (Bashir et al., 2020). These anthropogenic activities have resulted in the contamination of water sources through forms of bacteria and viruses, which are known as emerging pathogens due to their apparent virulence: pesticides, sludges, and sewages contaminated the soils of rivers and provided industrial discharges of chemicals and microelements, also becoming emerging pollutants of the environment and water bodies following industrialization (Mishra et al., 2023).
Among these sources of water pollution, industrial pollution is a leading cause within rivers:
globally, numerous people perceive and utilize water bodies as an “industrial dustbin” for discarding industrial effluents without bearing the extreme environmental cost (Igwe et al., 2017). It is the negative externality of industries avoiding corporate social responsibilities that continues to aggravate the problematic effect of industrial pollution. Sewage is the greatest volume of waste discharged into the aquatic ecosystems, of which the majority originate from industrial practices: as industries emit 80% of municipal wastewater into river bodies without filtration, millions of tons of heavy metals and toxic sludge eventually reach river bodies (Bashir et al., 2020). When exemplifying the case study on the Ganga River, bioaccumulation and biomagnification from industrialization and urbanization have placed human health and welfare in danger, highlighting the necessity for reducing industrial effluent released into the Ganga River (Roy & Shamim, 2020).
The assessment of water quality is significant in determining the level of pollution within an area and understanding its impacts; to calculate and quantify water quality, specific parameters of waters are measured. Conventionally, the water quality of a water body is considered to be accurately determined through a ‘water quality index’, or a WQI. In a study of 30 different WQIs and their characteristics, the indices are able to be organized into three categories: a fixed system of parameters, an open system where basic parameters are recommended but not limited to, and a mixed system in which consists of both basic and additional parameters (Sutadian et al., 2015). An observation could be deduced from the comparison that the nearly all WQIs commonly included parameters such as potential for Hydrogen (pH), Dissolved Oxygen (DO), Biochemical Oxygen Demand (BOD), Chemical Oxygen Demand (COD) and Total Solids (TS) (Sutadian et al., 2015). These physicochemical and biological parameters, according to multiple authors, vary seasonally. Moreover, anthropogenic activities, soil erosion and waste deposited into rivers have been identified as factors influencing one or more of the parameters, showcasing that a multitude of variables are able to affect the measurements of the parameters (Igwe et al., 2017). To interpret individually, Total Dissolved Solids (TDS), a particular type of TS, includes substances from domestic and industrial waste as well, resulting in a positive correlation with industrialization (Rusydi, 2018); the case study in Medlock River of Great Manchester, United Kingdom revealed the negative correlation between DO levels industrial land and a positive relationship with woodlands, whereas BOD had increased in concentration when wastewater was discharged into the river (Nguyen et al. et al., 2023); COD concentration had risen in the Anzali Wetland, Iran due to seasonal climate change (Tahershamsi et al., 2009); lastly, a decrease in the pH values could be observed in the Guadiamar River following the 1998 Aznalcóllar spill in Andalusia, Spain that raised the toxicity of the water, revealing a connection between pH and industrial discharges as well (M. Olías et al., 2005).
The Han River runs throughout South Korea and passes through multiple cities, from the riverhead Geomryongso, Taebaek to the Yellow Sea. It is a significant aspect of South Korea, supplying clean water to over 20 million people solely within Seoul, the nation’s capital (Lee et al., 2019). Occupying a watershed area of 26200 km2, the Han River has been straightened to be of 469.7 km in length for water control and presents a diverse ecosystem that should be maintained; yet the continual reduction in species such as the Korean eel (Anguilla japonica) indicates the threat faced by its ecosystem due to environmental degradation and pollution (Lee et al., 2019). The Han River is also extremely significant in the cultural context by providing aid throughout the development and settlement of the Korean civilization in addition to the economic benefits a long, controlled river provides (Lee et al., 2019). The management of the Han River is strictly managed by the South Korean government, as the river is an essential aspect of the nation. Subsequent to the industrialization of the nation, the government had recognized the importance of water quality management and undertook “multi-purpose dam” construction projects in the upstream region of the Han River while enacting five new regulations to protect the river (Shin et al., 2016). However, the management of the Han River has been increasing in difficulty as the water quality of the river body appeared to deteriorate. In particular, the eutrophication of the Han river is a substantial concern when managing the river’s water quality: the decline in BOD/COD ratio between 1986 and 2006 displays the increase in the proportion of recalcitrant organic matter, suggesting of a possibility of eutrophication of the river exacerbating(Shin et al., 2011). On the contrary, a decreasing trend of BOD levels could be observed due to the newly implemented sewage treatment facilities (Shin et al., 2011). Such evolved methods of regulation of the environment have begun to emerge in South Korea, invoked by the heightening of the pollution levels. As one of the selected procedures since the 1970s, Integrated Water Resource Management (IWRM) approaches are environmentally sustainable and considers human necessities (Hwang et al., 2020). Clearly illustrated by this study, methods of measuring and maintaining water quality become increasingly important as the consequential effects of environmental pollution become more drastic and complex.
The Donau River extends through numerous European nations, beginning in the Black Forest mountains of Germany and flowing until reaching the Black Sea. It is similarly significant to Austria as the second-largest river in Europe, stretching over a great distance of 2,845 km and critically influencing the ecological and economical landscape (Dávid & Madudová, 2019). Providing residence for diverse species of flora and fauna including endangered animals, the Donau river’s biodiversity appears to consist of over 320 avian species and a larger distinction among reptiles and amphibians (Vynokurova et al., 2023). The Danube River contributed to shaping the culture of Austria through various characteristics, allowing for “cultural, ethnic and political diversity” within the Donau River Basin (Schmid et al., 2023).
Similar to the Han River, the Austrian government provides management of the Donau River, but numerous organizations have implemented various ways of preserving it. The European Union’s enactment of the Water Framework Direction (WFD) exemplifies such involvement, proposing guidelines for a vast majority of European nations to follow (Stagl & Hattermann, 2015). Even so, as the urbanization of the nation continues, its environment continues to be damaged: within the last two centuries, the floodplain of the river has declined to less than 19% of the original size, demonstrating a decrease from 41605 km2 to 7845 km2 (Habersack et al., 2015). This decrease is detrimental, since most countries adjacent to the Donau River Basin generate over 45% of their hydropower through the Donau River Basin (Habersack et al., 2015). Furthermore, the contamination of the river’s water itself presents a further significant impact. The pollution of the river causes changes to the hydrodynamics of the river and restricts the spawning areas of a great number of species (Habersack et al., 2015).
Consistent sampling of water quality is extremely important in long-term safeguarding of river bodies, providing a quantitative measurement of the river’s pollution, consequences of industrial discharge, and the effect of urbanization. Numerous research emphasizes the importance of monitoring the water quality of rivers that reveals their current state. “Regular review of environmental effects of surface water pollution should be conducted by researchers to indicate the trend in pollutional loads of rivers, stream and lakes across the globe” (Igwe et al., 2017); “the evaluation of biological diversity have been recognized as an important national task to establish bio-sovereignty in the world” (Lee et al., 2019); “The paper emphasizes the importance of ensuring safe and clean drinking water through robust water treatment and monitoring systems” (Mohamed, 2024). Considering the implication above, this paper showcases a comparison of water quality and the effect of industrial pollution on the Han and Donau River, allowing important conclusions to be drawn from the two rivers located in hugely distinct settings. The research utilizes the parameters of DO, pH and TDS within the river bodies to evaluate the water quality of the Han and Donau River, supported with identified factors of industrial pollution.
2. Untersuchungsgebiet, Materialien und Methoden
2.1 Geographische Lage
Die Datenerhebung für den Han-Fluss konzentrierte sich ausschließlich auf die Umgebung von Seoul. In ähnlicher Weise wurden in dieser Studie Daten aus der Region Wien gesammelt. Die Auswahl der Datenerhebungsstellen war durch geografische Herausforderungen eingeschränkt; daher wurden die Han- und Donau-Flüsse in drei Segmente unterteilt: Oberlauf, Mittellauf und Unterlauf. Die Flussläufe wurden jeweils von der Mitte Seouls in Südkorea und Wiens in Österreich aus in drei Teile geteilt, mit einer ungefähren Einheit von 20 km zwischen den Datenerhebungsstellen. Konkret wurden zwei Standorte jedes Segments homogen so ausgewählt, dass sie sich direkt gegenüberlagen, um Variationen in den erhobenen Daten durch Bodenerosion, Wasserströmungen und geologische Gegebenheiten zu berücksichtigen. Die Standorte wurden nach Zugänglichkeit ausgewählt, da der Großteil des Flusseinzugsgebiets nur eingeschränkt zugänglich war. Daher unterschieden sich die ausgewählten Standorte leicht bei der Erhebung von DO, pH und TDS. Da die Höhe ein wesentlicher Faktor ist, der die physikochemischen Parameter eines Flusses beeinflusst, wurde die Höhe der Standorte über dem Meeresspiegel mithilfe einer mobilen Anwendung erfasst. Die Höhenlage der Datenerhebungsstellen erschien konsistent, und es gab nur minimale Unterschiede zwischen den beiden Flüssen. Ein weiterer zu berücksichtigender Faktor ist die zeitliche Lage der Datenerhebung. Die DO-Daten wurden im August und September 2023 erhoben; TDS- und pH-Daten wurden zwischen Ende Juni und Anfang August 2024 gesammelt. Somit wurden alle Daten während der Regenzeiten erhoben, in denen Elemente wie Regen und Temperatur Schwankungen in den Messergebnissen verursachen können, die berücksichtigt werden sollten. Die Lage der Datenerhebungsstellen ist in Tabelle 1 zusammengefasst. Das spezifische geologische Gebiet der Datenerhebung ist in Abbildungen 1 und 2 dargestellt.
Tabelle 1. Lage der Datenerhebungsstellen.

Abbildung 1. Karte der DO-Datenerfassungsstandorte.
Abbildung 1. Karte der DO-Datenerfassungsstandorte.

Abbildung 2. Karte der pH- und TDS-Datenerfassungsstandorte.
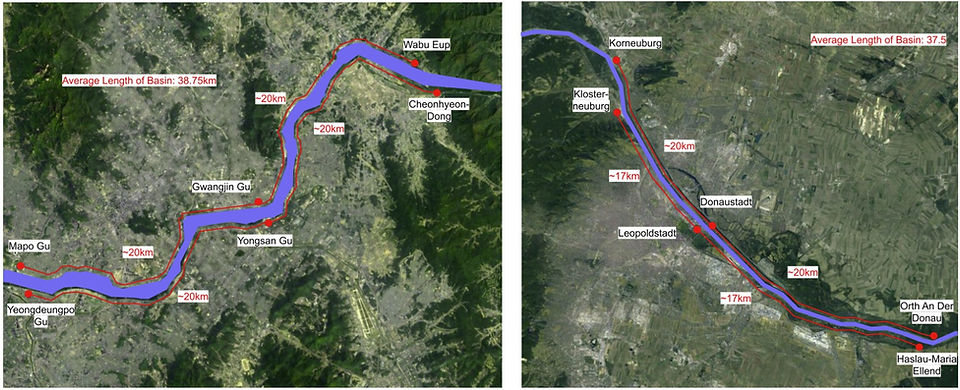
Fußnote: Verwendete Google-Satellitenbilder (Google Maps, 2019)
2.2 Datenerhebung
Die Daten wurden mit einer handgefertigten Teleskopstange gesammelt, die das Entnehmen von 100-ml-Proben von Oberflächenwasser aus den Flüssen in einer Tiefe von 5 Metern an jedem Erhebungspunkt ermöglichte. Zur Messung des Gelösten Sauerstoffs (DO) wurde ein Milwaukee Dissolved Oxygen Meter verwendet, während pH und Gesamte Gelöste Feststoffe (TDS) mit einem Virph Digital Water pH TDS Temperature Meter gemessen wurden. Ein digitales Wasserthermometer (CAS) wurde eingesetzt, um die Temperatur der Proben zu erfassen. DO-Messungen wurden in Abständen von einer Minute erhoben und innerhalb von drei Tagen nach der Probenahme ex-situ aufgezeichnet, was zu 150 Versuchen pro Standort führte. Während der Erhebung von pH- und TDS-Daten wurden die Werte konstant von zwei Sensoren alle 30 Sekunden für jeweils 75 Versuche aufgezeichnet, wodurch Schwankungen in den Daten minimiert und eine in-situ-Erhebung ermöglicht wurde, da das Intervall kürzer und die Anzahl der Versuche geringer war. Die Daten und Probenahmedaten wurden dokumentiert und sind in Tabelle 2 und 3 dargestellt.
Tabelle 2. Datum der DO-Proben und Datenerhebung.
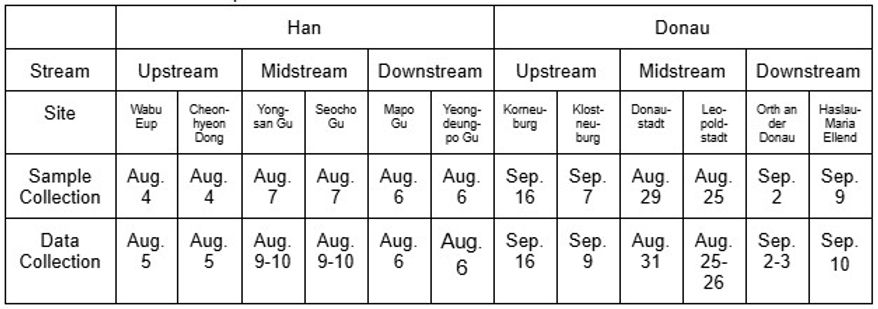
Tabelle 3. Datum der pH- und TDS-Proben und Datenerfassung.

2.3 Modellierungsmethodik
In der Studie wurden drei Modelltypen implementiert, um das genaueste Modell zur Vorhersage industrieller Verschmutzung auf Basis verschiedener Parameter zu identifizieren: lineare Modelle, Support-Vector-Modelle und Ensemble-Modelle. Die Python-Bibliothek Scikit-Learn wurde für diese Forschung verwendet, da sie mehrere Basismodelle, Methoden der Merkmalsauswahl und Techniken der Dimensionsreduktion bereitstellt (Buitinck et al., 2013).
2.3.1 Lineare Modelle
Für lineare Modelle wurden sechs Regressionen als Regressoren/Klassifikatoren verwendet – lineare Regression, Single-Layer Perceptron, Lasso-Regression, Ridge-Regression, Elastic-Net-Regression und lineares SVR. Lineare Modelle verwenden im Allgemeinen die unten angegebene Gleichung, um das Modell anzupassen. Gleichung 1 beschreibt ein lineares Modell, bei dem Vorhersagen durch die Summierung gewichteter Eingangsmerkmale und eines Bias-Terms gebildet werden. Diese Struktur geht von einer direkten, proportionalen Beziehung zwischen Variablen und Ausgabe aus, was sie zu einem grundlegenden Ansatz im maschinellen Lernen macht. Häufig für Regression und binäre Klassifikation eingesetzt, unterstützt die Einfachheit des Modells Interpretierbarkeit und Rechengeschwindigkeit. Aufgrund seiner Abhängigkeit von Linearität ist es jedoch nur eingeschränkt geeignet, komplexe Muster zu erfassen. Dennoch dient das lineare Modell weiterhin als Basis in der empirischen Modellierung, insbesondere wenn Transparenz und einfache Implementierung Vorrang vor nichtlinearer Vorhersagekraft haben.
Gleichung 1. Lineares maschinelles Lernmodell

Die lineare Regression ist aufgrund ihrer Einfachheit eine der am häufigsten verwendeten Formen der „Regression“. Wie der Name schon sagt, ist das Modell eine bestangepasste lineare Linie basierend auf gegebenen Datenpunkten, und die unten angegebene lineare Gleichung kann verwendet werden, um einen bestimmten Parameter „vorherzusagen“. Zur Optimierung wird typischerweise die Methode der kleinsten Quadrate (OLS) verwendet. Gleichung 2 skizziert das Regressionsmodell der kleinsten Quadrate (OLS), das die lineare Beziehung zwischen einer abhängigen Variable und mehreren Prädiktoren schätzt. Jeder Koeffizient spiegelt den Randeffekt eines Prädiktors wider, während der Fehlerterm die unerklärliche Varianz berücksichtigt. Durch Minimierung der quadrierten Residuen liefert OLS unter klassischen Annahmen effiziente Schätzwerte. Aufgrund ihrer Klarheit und Interpretierbarkeit bleibt diese Methode für die empirische Analyse fachübergreifend von zentraler Bedeutung. Ihre Leistung kann jedoch bei Multikollinearität oder Heteroskedastizität nachlassen, was eine diagnostische Bewertung und in einigen Fällen den Einsatz von Regularisierungs- oder Transformationstechniken zur Sicherstellung der Validität erforderlich macht.
Gleichung 2. OLS-Gleichung

Das Single-Layer-Perceptron (SLP) ist eines der ersten Modelle für die Klassifizierung, insbesondere in binären Umgebungen. Als grundlegende neuronale Einheit basiert es auf der Anpassung der Modellgewichte anhand von Vorhersagefehlern während des Trainings. Gleichung 3 beschreibt die vom Perceptron verwendete Lernregel, die die Gewichte durch Hinzufügen einer skalierten Version des Eingabevektors aktualisiert, wenn die vorhergesagte Ausgabe nicht mit der tatsächlichen Bezeichnung übereinstimmt. Obwohl das Perceptron auf linear separierbare Probleme beschränkt ist und keine komplexen Entscheidungsgrenzen modellieren kann, bleibt es ein grundlegendes Konzept für die Entwicklung neuronaler Netzwerke und moderner Deep-Learning-Systeme.
Gleichung 3. SLP-Lernalgorithmus

Die Lasso-Regression erweitert den traditionellen linearen Regressionsansatz um eine Regularisierungskomponente zur Förderung der Spärlichkeit. Insbesondere enthält das Modell eine L1-Strafe, die die Summe der Absolutwerte der Koeffizienten begrenzt. Gleichung 4 stellt diese Verlustfunktion dar, wobei der Strafterm bestimmte Koeffizienten effektiv auf Null reduziert. Dies macht Lasso besonders nützlich in Situationen mit einer großen Anzahl von Prädiktoren, da es gleichzeitig Variablenauswahl und Regression durchführt. Die Methode kann jedoch instabil werden, wenn die Prädiktoren stark korreliert sind, da sie dazu neigt, einen Prädiktor auszuwählen und andere willkürlich zu verwerfen, was ihre Robustheit in solchen Situationen einschränkt.
Gleichung 4. Lasso-Regressionsgleichung (L1-Regularisierung)

Die Ridge-Regression bietet eine Alternative zu Lasso, indem sie eine L2-Strafe zur Regularisierung der Modellkoeffizienten verwendet. Im Gegensatz zu Lasso setzt Ridge die Koeffizienten nicht auf Null, sondern reduziert sie auf Null, was Überanpassung und Multikollinearität reduzieren kann. Wie in Gleichung 5 gezeigt, bestraft die Verlustfunktion die quadrierten Größen der Koeffizienten und fördert so kleinere und ausgewogenere Parameterwerte. Dieser Ansatz eignet sich besonders für Situationen, in denen die Beibehaltung aller Prädiktoren bevorzugt wird, beispielsweise wenn die Interpretierbarkeit der allgemeinen Vorhersageleistung untergeordnet ist.
Gleichung 5. Ridge-Regressionsgleichung (L2-Regularisierung)

Die Elastic-Net-Regression kombiniert die Stärken von Lasso und Ridge und verwendet eine gewichtete Summe ihrer jeweiligen Strafen, um ein Gleichgewicht zwischen Spärlichkeit und Stabilität zu erreichen. Die resultierende Verlustfunktion, dargestellt in Gleichung 6, ermöglicht die Variablenauswahl und berücksichtigt gleichzeitig Multikollinearität, die weder Lasso noch Ridge allein optimal bewältigen. Dieser Dual-Penalty-Ansatz ist besonders vorteilhaft bei hochdimensionalen Datenkonstellationen, in denen viele Prädiktoren korreliert sind. Durch die Anpassung der Gewichte der L1- und L2-Komponenten kann das Modell an spezifische Dateneigenschaften angepasst werden und bietet so eine flexible Lösung für komplexe Regressionsaufgaben.
Gleichung 6. Elastische Nettoregressionsgleichung (L1 + L2-Regularisierung)

Die lineare Support Vector Regression (SVR) weicht von Standardregressionsmethoden durch die Einführung einer Epsilon-unempfindlichen Marge ab, innerhalb derer Vorhersagefehler nicht bestraft werden. Die in Gleichung 7 angegebene Vorhersagefunktion ähnelt der anderer linearer Modelle, ist jedoch anders optimiert. Anstatt den quadrierten Fehler zu minimieren, konzentriert sich SVR auf die Suche nach einer Funktion, die zu den Daten passt und gleichzeitig kleine Abweichungen toleriert. Dieser Ansatz erhöht die Robustheit gegenüber Ausreißern und kleinen Schwankungen in den Daten und macht SVR besonders geeignet für Aufgaben, die hohe Präzision bei begrenzten Fehlermargen erfordern, wie z. B. Finanzprognosen oder die Modellierung von Steuerungssystemen.
Gleichung 7. Lineare SVR-Vorhersagefunktion
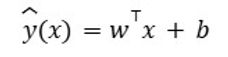
2.3.2 Nichtlineare Support-Vektor-Modelle
Der nichtlineare Support Vector Regressor (SVR) erweitert das lineare SVR-Framework durch die Integration von Kernelfunktionen und ermöglicht so die Erfassung komplexer, nichtlinearer Beziehungen in den Daten. In dieser Studie wurden Nu- und Epsilon-SVR als nichtlineare SVRs verwendet.
Gleichung 8 stellt die Vorhersagefunktion für nichtlineare SVR dar, bei der Eingabemerkmale durch einen Kernel in einen höherdimensionalen Raum abgebildet werden, was eine lineare Trennung in diesem transformierten Raum ermöglicht. Die Vorhersage wird durch eine gewichtete Summe von Support-Vektoren und ihren entsprechenden Koeffizienten sowie einem Bias-Term bestimmt. Diese Formulierung ermöglicht SVR die Modellierung komplexer Muster bei gleichzeitiger Wahrung der Robustheit, insbesondere bei Anwendungen mit unregelmäßigen oder stark variablen Datensätzen.
Gleichung 8. Nichtlineare SVR-Vorhersagefunktion
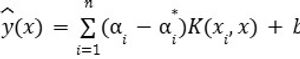
Zur Implementierung nichtlinearer SVR werden Kernelfunktionen verwendet, um Daten implizit in höherdimensionale Räume zu projizieren. Polynomkerne, dargestellt in Gleichung 9, erfassen gekrümmte Entscheidungsgrenzen, indem sie das Skalarprodukt von Eingabevektoren auf einen festen Grad erhöhen. Der in Gleichung 10 beschriebene Radial Basis Function (RBF)-Kernel ist einer der am häufigsten verwendeten Kernel. Er wendet ein Gaußsches Ähnlichkeitsmaß an, das lokale Muster hervorhebt. Gleichung 11 führt den Sigmoid-Kernel ein, der neuronale Aktivierungsfunktionen nachahmt und gelegentlich in netzwerkbasierten Modellen verwendet wird. Gleichung 12 stellt den Kosinus-Kernel dar, der die Ausrichtung statt der Größe von Vektoren vergleicht und sich daher für Text und hochdimensionale spärliche Daten eignet. Diese Kernel unterscheiden sich in ihren geometrischen Annahmen und ihrer Rechenkomplexität, was Modellflexibilität in unterschiedlichen Domänen ermöglicht.
Gleichung 9-13. Nichtlineare Kernel

Beim Training mit nichtlinearen Kerneln kann die resultierende Kernelmatrix – auch Gram-Matrix genannt – vorab berechnet und gespeichert werden, um die Vorhersage zu beschleunigen, insbesondere bei der Arbeit mit festen Trainingsdatensätzen. Gleichung 14 beschreibt, wie Vorhersagen direkt aus der vorab berechneten Kernelmatrix getroffen werden können, indem die erlernten dualen Koeffizienten auf den Testdatensatz angewendet werden. Diese Methode ist nützlich bei umfangreichen Anwendungen oder Szenarien, die wiederholte Vorhersagen erfordern und bei denen die Laufzeiteffizienz ein entscheidender Faktor ist. Durch die Nutzung der Struktur der Kernelmatrix behält das Modell seine Genauigkeit bei und verbessert gleichzeitig die Rechenleistung.
Gleichung 14. Vorkalkulierte Kernelmatrix-Testvorhersagefunktion
2.3.3 Modellensembles
Anstatt sich auf ein einzelnes Modell zu verlassen, kombinieren Ensemble-Methoden mehrere Lernalgorithmen zu einem zusammengesetzten Modell, das die Stärken jeder einzelnen Komponente nutzt. Die fünf in dieser Studie verwendeten Modell-Ensembles waren Adaptive Boosting Regressor (ABR), Bagging Regressor (BR), Gradient Boosting Regressor (GBR), Histogram-based Gradient Boosting Regressor (HGBR) und Random Forest Regressor (RFR).
ABR kombiniert mehrere schwache Lerner, um ein stärkeres Vorhersagemodell zu bilden, indem zuvor falsch vorhergesagte Instanzen hervorgehoben werden. Gleichung 15 stellt die ABR-Vorhersagefunktion dar, wobei jeder schwache Lerner mit einer zugehörigen Gewichtung zum endgültigen Ergebnis beiträgt. Das Ensemble konzentriert sich sequenziell auf Restfehler und verfeinert so schrittweise die Genauigkeit des Modells. ABR ist besonders effektiv bei Daten mit komplexen Fehlerverteilungen, da es sich durch Neugewichtung der Trainingsbeispiele an schwierige Fälle anpasst. Die allgemeine Effektivität von ABR liegt in seiner iterativen Fehlerkorrektur und seiner Fähigkeit, Verzerrungen in unterangepassten Basismodellen zu reduzieren. Die Wahl der Verlustfunktion in ABR bestimmt, wie Fehler während der Modellkonstruktion bestraft werden. Gleichung 16 definiert einen linearen Verlust, der den Vorhersagefehler direkt bestraft und so Einfachheit, aber begrenzte Robustheit bietet. Gleichung 17 führt eine quadrierte Verlustfunktion ein, die größere Abweichungen verstärkt und empfindlich auf Ausreißer reagiert. Alternativ bestraft der exponentielle Verlust in Gleichung 18 Fehlvorhersagen aggressiv und untermauert den ursprünglichen AdaBoost-Algorithmus, indem er den Fokus auf falsch vorhergesagte Stichproben erhöht. Jede Verlustfunktion verändert die Art und Weise, wie sich das Ensemble an Fehler anpasst, und beeinflusst sowohl die Modellsensitivität als auch das Konvergenzverhalten.
Gleichung 15-18. ABR-Gleichungen

BR aggregiert Vorhersagen mehrerer Basismodelle, die auf Bootstrap-Teilmengen der Daten trainiert wurden. Die in Gleichung 19 beschriebene Vorhersageregel berechnet den durchschnittlichen Output aller Einzelmodelle, wobei jedes Modell den gleichen Beitrag leistet. Dieser Ensemble-Ansatz reduziert die Varianz, ohne die Verzerrung signifikant zu erhöhen, und verbessert so die Modellstabilität und -leistung bei verrauschten Daten. Bagging ist besonders nützlich in Szenarien, in denen einzelne Modelle überangepasst sind, da der Mittelungsprozess dazu neigt, durch Datenschwankungen verursachte Unregelmäßigkeiten auszugleichen.
Gleichung 19. BR-Vorhersagegleichung
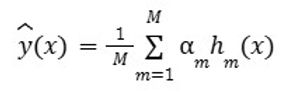
GBR erstellt iterativ Modelle, indem jeder neue Lerner an die Residuen der Vorhersagen des vorherigen Ensembles angepasst wird. Gleichung 20 formalisiert diesen additiven Prozess, bei dem das Modell durch Kombination der vorherigen Vorhersage mit einer skalierten Fehlerreduzierungsfunktion aktualisiert wird. Dieser Ansatz ermöglicht es GBR, das Lernen auf Bereiche zu konzentrieren, in denen vorherige Modelle unterdurchschnittlich abschnitten. Seine Flexibilität bei der Optimierung verschiedener Verlustfunktionen macht es breit anwendbar bei strukturierten Datenaufgaben wie Ranking-, Regressions- und Klassifizierungsproblemen mit Nichtlinearität und Merkmalsinteraktionen. Die Effektivität von GBR hängt stark von der Verlustfunktion ab, die es optimiert. Gleichung 21 beschreibt den mittleren quadratischen Fehler (MSE), die aufgrund ihrer Empfindlichkeit gegenüber großen Fehlern am häufigsten für die Regression gewählt wird. Der mittlere absolute Fehler (MAE), dargestellt in Gleichung 22, behandelt alle Abweichungen gleich und bietet Robustheit gegenüber Ausreißern. Der Huber-Verlust in Gleichung 23 vereint beide Ansätze, indem er kleine Fehler quadratisch und große Fehler linear bestraft, wodurch er sich für verrauschte Daten eignet. Gleichung 24 führt die Quantilverlustfunktion ein, die es dem Modell ermöglicht, bedingte Quantile statt Durchschnittsergebnisse vorherzusagen, eine wertvolle Funktion bei Prognoseintervallen und risikosensitiven Anwendungen.
Gleichung 20-24. GBR-Gleichungen

HGBR optimiert GBR durch die Diskretisierung kontinuierlicher Merkmale in Histogramme, was eine schnellere Berechnung und Speichereffizienz ermöglicht. Gleichung 25 zeigt die Aktualisierungsregel, bei der jede Iteration dem Modell mithilfe einer Lernrate einen neuen Lerner hinzufügt. Gleichung 26 stellt die minimierte Verlustfunktion dar, häufig den Quantilsverlust, der es HGBR ermöglicht, robuste Regressionen bei asymmetrischen Fehlerverteilungen durchzuführen. Dieses Design macht HGBR besonders effizient für große Datensätze und bietet gleichzeitig Flexibilität im Umgang mit verzerrten Zielen und Fehlern mit schweren Rändern, ein häufiges Problem bei angewandten Prognoseproblemen.
Gleichung 25-26. HGBR-Gleichungen

RFR prognostiziert Ergebnisse durch Mittelung der Ergebnisse mehrerer Entscheidungsbäume, die mit zufälligen Datenteilmengen und Merkmalsauswahlen trainiert wurden. Gleichung 27 definiert diesen Aggregationsprozess, bei dem jeder Baum unabhängig ein Ergebnis vorhersagt und das Ensemble diese durch Mittelung kombiniert. RFR mildert Überanpassung durch die Einführung von Zufälligkeit und reduziert die Varianz durch Ensemble-Lernen. Seine Fähigkeit, komplexe, nichtlineare Beziehungen ohne umfangreiche Vorverarbeitung zu modellieren, hat es zu einer bevorzugten Methode in Bereichen von der Ökologie über die Finanzwelt bis hin zur klinischen Forschung gemacht.
Gleichung 27. RFR-Vorhersagegleichung

2.3.4 Methoden zur Merkmalsauswahl
Die fünf bei den Modellen angewandten Methoden zur Merkmalsauswahl waren Chi-Quadrat-Test, F-Test/Varianzanalyse (ANOVA), Mutual-Information-Test (MIT), Pearson-Korrelationskoeffizient und rekursive Merkmalseliminierung (RFE).
Der Chi-Quadrat-Test, eingeführt in Gleichung 28, ist ein statistisches Verfahren, um zu bestimmen, ob beobachtete Verteilungen über kategoriale Gruppen signifikant von den bei Unabhängigkeit zu erwartenden Abweichungen abweichen. Er wird häufig in der Kontingenztafelanalyse eingesetzt und prüft, ob Abweichungen in Häufigkeitszählungen zufällig entstehen. Dieser Test ist besonders nützlich im Klassifizierungskontext, wo er zur Bewertung der Relevanz kategorialer Merkmale eingesetzt werden kann. Ein höherer Wert der Teststatistik weist typischerweise auf eine stärkere Abhängigkeit zwischen Variablen hin und bietet eine Grundlage für die Merkmalsauswahl oder Hypothesenprüfung.
Gleichung 28. Chi-Quadrat-Test

Gleichung 29 definiert den F-Test, ein grundlegendes Element der Varianzanalyse. Dieser Ansatz bewertet, ob die durch Gruppenunterschiede erklärte Variabilität die Restvariation innerhalb dieser Gruppen übersteigt. Bei Anwendung auf kontinuierliche Prädiktoren, die nach einem kategorischen Ergebnis segmentiert sind, hilft der Test, Variablen mit signifikanter Trennschärfe zu identifizieren. Er ist besonders effektiv in Regressions- oder Klassifikationspipelines, wo die Auswahl von Merkmalen, die eine erhebliche Varianz zwischen Gruppen erklären, die Interpretierbarkeit und Leistung des Modells verbessern kann.
Gleichung 29. F-Test (ANOVA)

MIT, dargestellt in Gleichung 30, bietet einen nichtparametrischen Ansatz zur Quantifizierung der gemeinsamen Abhängigkeit zwischen Variablen. Im Gegensatz zu korrelationsbasierten Methoden erfasst es sowohl lineare als auch nichtlineare Beziehungen und eignet sich daher zur Erkennung komplexer Zusammenhänge. Dieses Maß wird häufig bei der Merkmalsauswahl verwendet, um Prädiktoren zu identifizieren, die im Vergleich zum Ziel einen erheblichen Informationsgewinn bieten. Seine Flexibilität über verschiedene Datentypen hinweg macht es besonders wertvoll in Bereichen mit gemischten oder nicht-Gaußschen Verteilungen.
Gleichung 30. MIT-Gleichung
Gleichung 31 stellt ein statistisches Maß dar, das den Grad der linearen Assoziation zwischen zwei kontinuierlichen Größen quantifiziert. Durch den Vergleich ihrer Kovariabilität mit der individuellen Variabilität zeigt die Metrik, ob Anstiege einer Variablen mit systematischen Änderungen einer anderen einhergehen. Sie wird häufig in den frühen Phasen der Datenanalyse eingesetzt und dient als Filter zur Identifizierung von Redundanzen und kollinearen Merkmalen. Obwohl sie auf lineare Trends beschränkt und empfindlich gegenüber Ausreißern ist, bleibt sie eine der am häufigsten verwendeten Techniken zur Bewertung von Variablenbeziehungen.
Gleichung 31. Pearson-Korrelationsformel

Die rekursive Merkmalseliminierungsmethode, beschrieben in Gleichung 32, entfernt systematisch Prädiktoren, die am wenigsten zur Modellleistung beitragen. Bei jeder Iteration wird das Modell neu bewertet, um den Einfluss jedes verbleibenden Merkmals zu bestimmen. Dieser Ansatz ermöglicht die Verfeinerung der Modellkomplexität durch Priorisierung aussagekräftigerer Variablen. Er wird häufig in hochdimensionalen Kontexten eingesetzt und trägt dazu bei, Überanpassung zu vermeiden und die Generalisierung zu verbessern, insbesondere bei Modellen, die stark von der Eingangsdimensionalität abhängen.
Gleichung 32. RFE-Gleichung
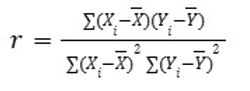
2.3.5 Dimensionality Reduction Techniques
Lastly, seven dimensionality reduction techniques were used as the last process of the two-layer feature selection, consisting of Principal Component Analysis (PCA), Incremental PCA (IPCA), Sparse PCA (SPCA), Kernel PCA(KPCA), Truncated Singular Value Decomposition (TSVD), Factor Analysis (FA) and Dictionary Learning (DL).
Principal Component Analysis (PCA), introduced in Equation 33, reduces data dimensionality by identifying new axes that capture the maximum variance within the dataset. The method begins with the construction of a covariance matrix, which represents the linear relationships among features. Equation 34 involves decomposing this matrix to extract directions that best explain variance. The final transformation, shown in Equation 35, projects the data onto these directions, generating a lower-dimensional representation that retains as much original information as possible. PCA is widely employed for visualization, noise reduction, and as a preprocessing step in machine learning pipelines.
Principal Component Analysis (PCA), introduced in Equation 33, reduces data dimensionality by identifying new axes that capture the maximum variance within the dataset. The method begins with the construction of a covariance matrix, which represents the linear relationships among features. Equation 34 involves decomposing this matrix to extract directions that best explain variance. The final transformation, shown in Equation 35, projects the data onto these directions, generating a lower-dimensional representation that retains as much original information as possible. PCA is widely employed for visualization, noise reduction, and as a preprocessing step in machine learning pipelines.
Equation 33-35. PCA equations

Inkrementelle PCA (IPCA) ist eine rechnerisch effiziente Erweiterung der PCA, die eine Dimensionsreduktion bei Streaming- oder großen Datensätzen ermöglicht. Gleichung 36 definiert, wie die Daten mithilfe einer Teilmenge von Hauptrichtungen näherungsweise rekonstruiert werden können. Gleichung 37 quantifiziert den Rekonstruktionsfehler und gibt an, wie viele Informationen bei der Reduzierung der Dimensionsanzahl verloren gehen. IPCA ist besonders vorteilhaft in Szenarien, in denen nicht der gesamte Datensatz gleichzeitig im Speicher gehalten werden kann, und bietet einen Kompromiss zwischen Präzision und Skalierbarkeit.
Gleichungen 36-37. IPCA-Näherungsdatengleichungen

Sparse PCA (SPCA) modifiziert die Standard-PCA durch die Einführung von Sparsity-Beschränkungen. Dadurch entstehen Hauptrichtungen, die von weniger Merkmalen abhängen. Dies verbessert die Interpretierbarkeit durch die Identifizierung lokalisierter Muster in den Daten. Gleichung 38 beschreibt die Approximation des ursprünglichen Datensatzes mithilfe eines reduzierten Satzes spärlicher Komponenten, während Gleichung 39 den resultierenden Rekonstruktionsfehler misst. SPCA wird häufig in hochdimensionalen Kontexten wie der Genomik oder Textanalyse angewendet, wo die Standard-PCA aufgrund der Einbeziehung aller Merkmale in jede Komponente die sinnvolle Struktur verschleiern kann.
Gleichungen 38-39. SPCA-Näherungsdatengleichungen

Kernel PCA (KPCA) verallgemeinert PCA, indem es nichtlineare Dimensionsreduktion durch Kernelmethoden ermöglicht. Gleichung 40 definiert eine Matrix von Ähnlichkeitswerten, die in einem implizit transformierten Merkmalsraum berechnet werden. Dadurch kann die Methode nichtlineare Beziehungen erfassen. Die Kernelmatrix wird anschließend, wie in Gleichung 41 dargestellt, zentriert, um sicherzustellen, dass die transformierten Daten den Mittelwert Null behalten. Gleichung 42 beschreibt, wie die Daten in diesen Merkmalsraum projiziert werden. KPCA ist besonders wertvoll, wenn die zugrunde liegende Struktur der Daten nicht linear separierbar ist, und eignet sich daher für Aufgaben wie Bildverarbeitung und Mustererkennung.
Gleichung 40-42. KPCA-Gleichungen

Die Truncated Singular Value Decomposition (TSVD), wie in Gleichung 43 gezeigt, erzeugt eine niedrigrangige Approximation eines Datensatzes, indem nur die signifikantesten singulären Komponenten beibehalten werden. Dadurch wird die Dimensionalität reduziert, während wichtige Strukturinformationen erhalten bleiben. Eine bemerkenswerte Anwendung von TSVD ist die Latent Semantic Decomposition (LSD), insbesondere in der Verarbeitung natürlicher Sprache, wo sie verwendet wird, um verborgene semantische Beziehungen in Term-Dokument-Matrizen zu extrahieren. Durch die Projektion von Textdaten in einen reduzierten Raum erfasst LSD zugrunde liegende Konzepte, die Muster in der Wortverwendung erklären, und ermöglicht so eine verbesserte Abfrage und Clusterbildung. Obwohl TSVD eine lineare Struktur voraussetzt und keine probabilistische Interpretation verwendet, wird es aufgrund seiner Effektivität beim Komprimieren und Aufdecken latenter Muster häufig in der Textanalyse, der Informationsabfrage und in Empfehlungssystemen eingesetzt, wo Datenspärlichkeit und -redundanz häufig sind.
Gleichung 43. TSVD LSE-Gleichung
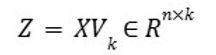
Die Faktorenanalyse (FA), dargestellt in den Gleichungen 44 und 45, modelliert beobachtete Daten als lineare Kombination latenter Faktoren und Rauschen. Dieser generative Ansatz geht davon aus, dass zugrunde liegende, nicht direkt messbare Variablen für Korrelationen zwischen beobachteten Merkmalen verantwortlich sind. Die Kovarianzstruktur wird durch die Beiträge dieser latenten Komponenten und einer diagonalen Fehlermatrix erklärt. Die FA wird häufig in psychologischen Tests, im Finanzwesen und anderen Bereichen eingesetzt, in denen unbeobachtete Konstrukte die beobachteten Ergebnisse beeinflussen sollen.
Gleichung 44-45. FA-Gleichungen

Dictionary Learning (DL), beschrieben in den Gleichungen 46–48, versucht, Daten als spärliche Kombinationen von Elementen aus einem optimierten Basissatz darzustellen. Die Zielfunktion minimiert Rekonstruktionsfehler und erzwingt gleichzeitig die Spärlichkeit der Darstellung. Zusätzliche Einschränkungen regulieren das Spärlichkeitsmuster über Merkmale oder Stichproben hinweg. Diese Methode ist besonders leistungsstark in der Signalverarbeitung, Bildkomprimierung und Sparse-Coding-Aufgaben, bei denen es darum geht, kompakte, aussagekräftige Darstellungen zu finden, die sowohl die Interpretation als auch die effiziente Speicherung erleichtern.
Gleichung 46-48. DL-Gleichungen

3. Ergebnisse und Diskussion
3.1 Qualitative Faktoren industrieller Verschmutzung
Wenn man die qualitativen Variablen industrieller Verschmutzung betrachtet, tragen verschiedene Faktoren zur Gesamtverunreinigung bei: So identifizierte eine Fallstudie des Karnafully-Flusses in Bangladesch Pestizide, feste Abfälle und Leckagen als die Hauptschadstoffe des Flusses, die aus nahegelegenen Industrien stammten (Bhuyan & Islam, 2017). Eine weitere Untersuchung des Ipojuca-Flusses in Brasilien hebt hervor, dass Zuckerrohrfabriken die Wassertemperatur erhöhten, organische Säuren den Fluss zusätzlich belasteten und überschüssiges Kalium aus Bewässerungsflüssigkeiten dazu führte, dass der Fluss mit biologisch abbaubaren Stoffen verunreinigt wurde (Gunkel et al., 2006). Solche Untersuchungen verdeutlichen, dass eine Vielzahl qualitativer Faktoren berücksichtigt werden muss, wenn industrielle Verschmutzung untersucht wird.
In Südkorea hat der Han-Fluss unter den großen Flüssen des Landes die meisten Verschmutzungsfälle verzeichnet und zwischen 2014 und 2018 insgesamt 283 Fälle angesammelt (Jung, 2019). In den letzten fünf Jahren wurden täglich 5494873 m³ Abwasser von den 24263 aktiven Anlagen produziert, von denen 3823429 m³ in den Han-Fluss geleitet wurden (Forschungsbericht – Untersuchung zur Aufstellung eines Schutzplans für das Han-Fluss-Mündungsgebiet (20-24)). Das Abwasser summiert sich zu 11 Millionen Tonnen behandeltem Abwasser, was die gesetzliche Grenze um 5 Millionen Tonnen überschreitet (An, 2022). Diese Verschmutzung führte auch dazu, dass der Han-Fluss als der weltweit 43. am stärksten mit Drogen belastete Fluss unter Gewässern aus 137 verschiedenen Ländern eingestuft wurde (Cho, 2023). Der Rückgang der Wasserqualität wurde seit den 1960er Jahren, als Südkorea mit der Industrialisierung begann, als erhebliches Problem hervorgehoben (Kim & Seoul National University Graduate School of Environmental Studies, 2024). Solche Informationen etablieren den Han-Fluss als ein stark von industrieller Verschmutzung betroffenes Gewässer.
Im Gegensatz dazu leidet Österreichs Donau scheinbar in geringerem Maße unter der Industrialisierung: Eine Bewertung aus dem Jahr 2009 stufte 22 % des Flusses als ökologisch in gutem Zustand und 45 % als chemisch in gutem Zustand ein (Gasparotti, 2014). Eine Studie, die die Unabhängigkeit von Fabriken von der Donau bei fortschreitender Industrialisierung annahm, wurde jedoch widerlegt, da sich die Wasserqualität des Flusses verschlechterte, weil Industrien in der Lage waren, ihre Abfälle aus größerer Entfernung in die Donau einzuleiten (Radu et al., 2020). Dieses Ergebnis stellt ein Gegenargument zur Annahme dar, dass die Donau generell weniger verschmutzt sei. Nichtsdestotrotz wurde festgestellt, dass 97,7 % des Wassers in Österreich von ausgezeichneter Qualität sind (Internationale Kommission zum Schutz der Donau, 2022). Die Bemühungen der Europäischen Union, die Wasserqualität des Flusses zu verbessern, haben dazu geführt, dass das Wasser für Aktivitäten wie Schwimmen sicher ist (Internationale Kommission zum Schutz der Donau, 2021). Daher deutet eine Vielzahl von Belegen auf eine vergleichsweise geringere industrielle Verschmutzung der Donau im Vergleich zum Han-Fluss hin.
3.2 Umweltvariablen
Die während der Erhebung der DO-Daten im Jahr 2023 aufgezeichneten Temperaturen der Oberflächenwasserproben schwankten zwischen 22,6 °C und 29,2 °C, mit einer maximalen Temperaturschwankung von 4,3 °C an jedem Standort. Insgesamt zeigte die Temperatur einen Trend, entweder zu steigen oder zu fallen, bis sie etwa 25 °C erreichte. Im Jahr 2024, während der Erhebung der pH- und TDS-Daten, schwankten die Temperaturen zwischen 24,5 °C und 30,5 °C. Die maximale Temperaturschwankung pro Standort war etwas höher als im Vorjahr und betrug 4,7 °C.
3.3 Physikochemische Parameter
Der Mittelwert, die Standardabweichung (SD) und der Standardfehler des Mittelwerts (SE Mean) der ausgewählten Parameter für die Wasserproben sind in den Tabellen 4 bis 7 dargestellt. Der DO-Wert lag knapp innerhalb des tolerierbaren Bereichs von 6,5 bis 8 mg/L, wobei das Minimum 6,660 mg/L und das Maximum 7,709 mg/L betrug; der pH-Wert schwankte zwischen 7,496 und 7,643; schließlich lag der TDS-Wert zwischen 83,912 und 196,628 ppm.
Tabellen 4-7. Statistische Zusammenfassung der Flussparameter.


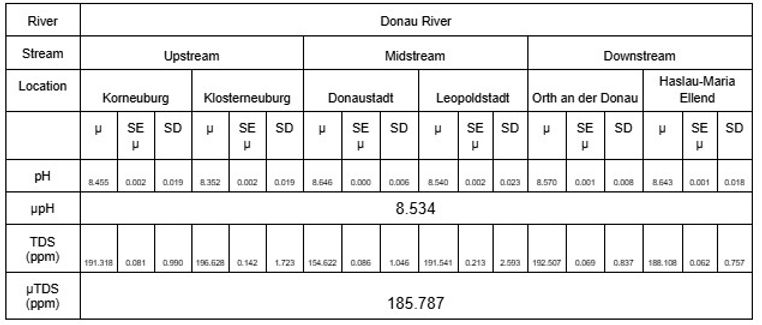
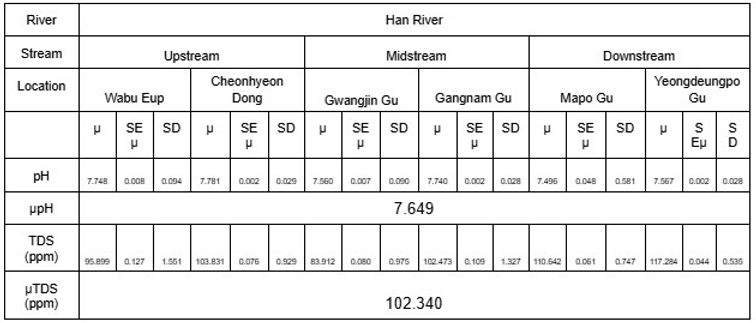
Die statistische Zusammenfassung untermauert die Behauptung, dass der Han-Fluss stärker durch Industrieverschmutzung verschmutzt ist als die Donau. Wie allgemein bekannt, werden niedrige DO- und TDS-Werte mit geringerer Wasserqualität und schwerer Verschmutzung eines Flusses in Verbindung gebracht, da sie auf einen Mangel an Ressourcen hinweisen, die das Leben im Wasser zum Überleben benötigt, und umgekehrt. Der Han-Fluss weist niedrigere mittlere DO- und TDS-Werte von 6,814 mg/l und 102,34 ppm auf als die Donau mit 7,502 mg/l und 185,787 ppm. Darüber hinaus gibt der pH-Wert den Säuregrad des Wassers an, wobei niedrigere Werte giftiger werden und auf eine Verschmutzung des Oberflächenwassers hinweisen. Der mittlere pH-Wert des Han-Flusses von 7,649 ist deutlich niedriger als der der Donau mit 8,534. Beide Beobachtungen belegen, dass der Han-Fluss im Vergleich zur Donau erheblich verschmutzt ist.
3.4 Bevölkerungsdichte
Die Bevölkerungsdichte misst die Einwohnerzahl eines bestimmten Gebiets und dient als indirekter Indikator für den Urbanisierungs- und Industrialisierungsgrad verschiedener Regionen. Insbesondere ermöglicht die Bevölkerungsdichte eine quantitative Schätzung der industriellen Verschmutzung: Eine am chinesischen Fluss Weihe durchgeführte Studie ergab einen Zusammenhang zwischen der Bevölkerungsdichte und industriellen Punktquellenabwässern (Zhang et al., 2012). Ebenso wurde die Bevölkerungsdichte mit Industrieemissionen im Mittelmeerraum in Verbindung gebracht, wo Gebiete mit hoher Bevölkerungsdichte als besonders anfällig für starke Verschmutzung gelten (Acar & Mahmut Tekce, 2014). Da die Bevölkerungsdichte als mögliche Methode zur Bewertung der industriellen Verschmutzung in den Flüssen Han und Donau genutzt werden kann, wurden in den in den Tabellen 8 bis 11 angezeigten Daten öffentliche Daten zur Bevölkerungsdichte von und Austria Statistik erfasst. HPD-Werte aus dem Jahr 2021 wurden bei der DO-Erhebung teilweise als HPD verwendet, da die österreichische Regierung die Bevölkerungszahlen der an Wien angrenzenden Regionen zwischen 2021 und 2024 nicht aktualisiert hat.
Tabellen 8-9. HPD der südkoreanischen und österreichischen Regionen der DO-Datenerhebung, 2021/2023

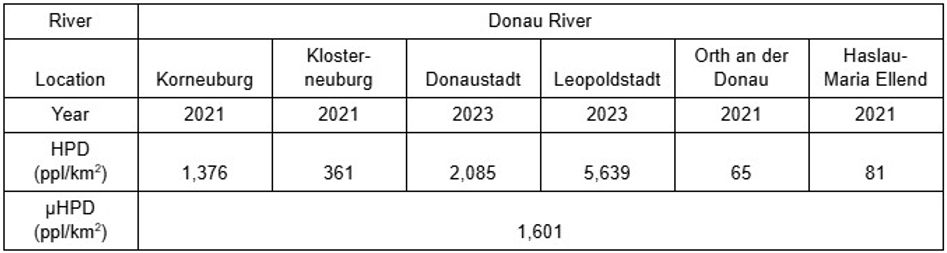
Tabellen 10-11. HPD der südkoreanischen und österreichischen Regionen zur Erfassung von pH- und TDS-Daten, 2024


Die Tabellen zeigen, dass die Bevölkerungsdichte (HPD) naturgemäß in den Regionen innerhalb der südkoreanischen Hauptstadt Seoul und der österreichischen Hauptstadt Wien höher ist. In Seoul wiesen Yongsan Gu, Seocho Gu, Gwangjin Gu und Gangnam Gu jeweils die höchsten HPD-Werte der erfassten Regionen auf, mit entsprechenden Werten von 9924, 8617, 19587 und 14090 Personen/km²; ähnlich waren Mapo Gu und Yeongdeungpo Gu nahe der Grenze Seouls ebenfalls stark bevölkert. Im Zentrum Wiens zeigten Donaustadt und Leopoldstadt HPD-Werte von 2085 und 5639 Personen/km² im Jahr 2023 sowie 2158 und 5722 Personen/km² im Jahr 2024. Die ländlichen Regionen der beiden Länder wiesen niedrige HPD-Werte zwischen 65 und 1160 Personen/km² auf. Insgesamt erscheint die Bevölkerungsdichte in Südkorea sowohl 2021 als auch in den Folgejahren deutlich höher gewesen zu sein als in Österreich, mit einem durchschnittlichen HPD des Han-Flusses von 8417 und 10918 Personen/km² im Vergleich zum Donau-Durchschnitt von 1601 und 1634 Personen/km², was zusätzlich verdeutlicht, dass der Han-Fluss stärkeren industriellen Verschmutzungsniveaus ausgesetzt war als die Donau.
3.5 Luftqualitätsindex
Der Luftqualitätsindex (AQI) liefert Informationen und Erkenntnisse über die Luftverschmutzung in einer bestimmten Region, indem er spezifische Schadstoffe in der Luft misst. Daher dient der AQI als Indikator für Verschmutzung und potenzielle Gesundheitsrisiken (Wu et al., 2021). Zu den üblichen Schadstoffen, die der AQI misst, gehören PM10, PM15, Schwefeldioxid und Kohlendioxid (Cairncross et al., 2007). Jeder dieser Schadstoffe ist gesundheitsschädlich, und die gesammelten Daten solcher Parameter werden zur Erstellung eines kumulativen Wertes, des AQI, genutzt. Während der grundlegende Luftqualitätsindex mit einer Skala von 0 bis 500 am häufigsten verwendet wird, nutzen bestimmte Regionen der Welt unterschiedliche AQI-Typen und -Metriken, um den Grad der Luftqualität und Verschmutzung in einem Gebiet zu bewerten. Abbildung 3 zeigt die AQI-Deskriptoren Südkoreas und der Europäischen Union (EU), zu der auch Österreich gehört (Wu et al., 2021).
Abbildung 3. AQI-Deskriptor von Südkorea und der EU
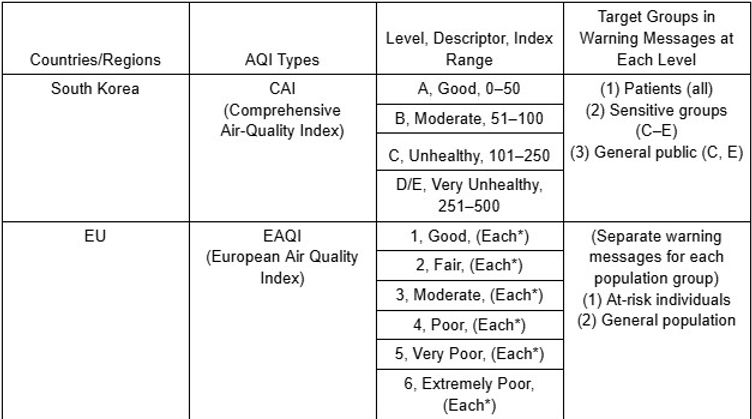
Da der AQI einen Aspekt der Verschmutzung innerhalb eines Gebiets darstellt, wurden öffentliche AQI-Daten des World Air Quality Index Project genutzt. Dabei wurden die Regionen der Datenerhebung nach Provinzen getrennt und die AQI-Werte des Datenerhebungstages von der nächstgelegenen Station zu den Datenerhebungsorten gemittelt. Da die EU nicht ausdrücklich angibt, welche Indexwerte zur Berechnung des EAQI verwendet werden, wurde der AQI-Deskriptor aus Südkorea herangezogen. PM2.5 und PM10 waren die beiden ausgewählten Parameter, da sie die am häufigsten vom AQI gemessenen Schadstoffe darstellen, während andere Parameter je nach Datenerhebungsstation variierten. Der CAI wurde berechnet, indem der höchste Wert ausgewählt und 50 addiert wurde, falls sowohl PM2.5 als auch PM10 in die Kategorien C, D oder E fielen; andernfalls wurde der höchste Wert als CAI ausgewählt (AirKorea: Introduction to the CAI, 2022). Die Tabellen 12 bis 15 fassen die aufgezeichneten öffentlichen Daten aus der DO-Datenerhebung im Jahr 2023 sowie der pH- und TDS-Datenerhebung im Jahr 2024 zusammen.
Tabellen 12-13. AQI der südkoreanischen und österreichischen Regionen der DO-Datenerhebung, 2023 (WAQI, 2008)


Tabellen 14-15. AQI der südkoreanischen und österreichischen Regionen der pH- und TDS-Datenerfassung, 2024 (WAQI, 2008)
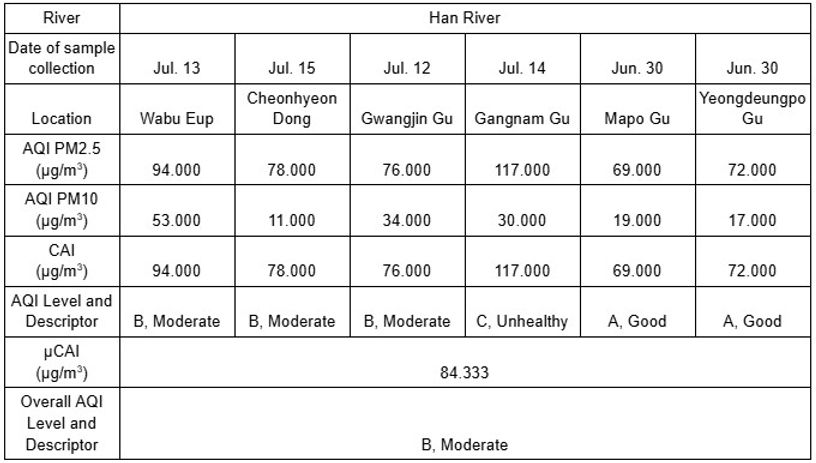

Bei der Interpretation der gesammelten AQI-Daten zeigten die CAI-Werte im Gegensatz zur HPD einen allgemeinen Trend in den Regionen der Datenerhebungsorte, anstatt in den Hauptstädten signifikant höher zu erscheinen. So wiesen Wabu-Eup und Cheonhyeon Dong während der Datenerhebungstage höhere CAI-Werte zwischen 56.000 und 94.000 μg/m³ auf als Mapo Gu und Yeongdeungpo Gu, die Werte zwischen 51.000 und 72.000 μg/m³ zeigten; die CAI-Werte von Klosterneuburg waren ebenfalls stark erhöht, 35.000 μg/m³ im Jahr 2023 und 31.000 μg/m³ im Jahr 2024, während Donaustadt eine äußerst saubere Luftqualität mit Werten von 23.000 und 28.000 aufwies. Solche Trends deuten darauf hin, dass der AQI nicht direkt mit urbanisierten Gebieten der Bevölkerung verbunden ist. Dieser Trend könnte jedoch auf die Untersuchung kleinerer Gebiete beschränkt sein, da die durchschnittlichen CAI-Werte der südkoreanischen Regionen die atmosphärische Bedingung als „B, Mäßig“ bewerteten und die österreichischen Regionen, die weniger bevölkert und industrialisiert sind als Südkorea, als „A, Gut“. Solche Gesamtergebnisse stützen weiterhin die Möglichkeit, dass der Han-Fluss im Vergleich zur Donau ein minderwertigeres Niveau industrieller Verschmutzung aufweist, da mehr Schadstoffe aus Industrien in die Luft freigesetzt werden.
3.6 Beziehung zwischen physikochemischen Parametern
Die Daten der ausgewählten physikochemischen Parameter wurden genutzt, um eine bivariate Korrelation zwischen den einzelnen Variablen aufzuzeigen. Mithilfe des Pearson-Produkt-Moment-Korrelationskoeffizienten wird eine Korrelationsmatrix der mittleren physikochemischen Parameter jedes Flusses in den Tabellen 16 und 17 dargestellt. Für HPD und AQI wurden die beiden Datensätze aus den Jahren 2023 und 2024 gemittelt, um für die Berechnung der Pearson-Koeffizienten verwendet zu werden.
Tabellen 16-17. Pearson-Produkt-Moment-Korrelationskoeffizienten-Matrix der physikochemischen Parameter des Han- und Donau-Flusses
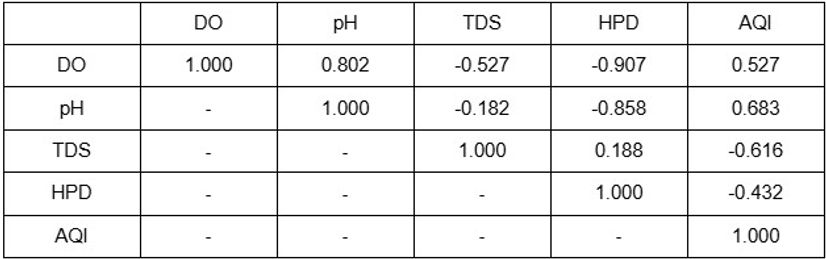

Eine allgemeine Faustregel bei der Interpretation von Pearson-Korrelationskoeffizienten ist, dass eine Korrelation als stark gilt, wenn der Betrag des Koeffizienten größer als 0,5 ist. Dennoch scheinen die Korrelationsmatrizen keine gemeinsamen Zusammenhänge aufzuzeigen. Während DO und pH im Han-Fluss einen hohen Pearson-Koeffizienten von 0,802 aufweisen, zeigt das Parameterpaar einen negativen Trend mit einem Koeffizienten von -0,858. Zudem scheint eine starke Korrelation innerhalb eines Flusses für den anderen schwach zu sein: Während Paare wie DO und HPD oder pH und HPD extrem starke negative Zusammenhänge von -0,907 und -0,858 zeigten, waren die Trends bei den Parametern der Donau nicht erkennbar, mit Koeffizienten von 0,254 und 0,084 für die jeweiligen Paare. Ebenso stand ein moderat hoher Koeffizient von 0,527 zwischen DO und AQI der Donau einem niedrigen Koeffizienten von 0,255 desselben Parameterpaars im Han-Fluss gegenüber. Somit präsentieren die beiden Korrelationsmatrizen den Vergleich zwischen verschiedenen Standorten desselben Flusses anhand der gegebenen Parameter als möglich, jedoch ungenau.
Um einen Überblick über die Beziehung zwischen den Parametern im Allgemeinen zu geben, wurde in Tabelle 18 eine alternative Korrelationsmatrix dargestellt, die kumulativ den Mittelwert der erhobenen Daten beider Flüsse verwendet.
Tabelle 18. Pearson-Produkt-Moment-Korrelationskoeffizienten-Matrix der physikochemischen Parameter beider Flüsse
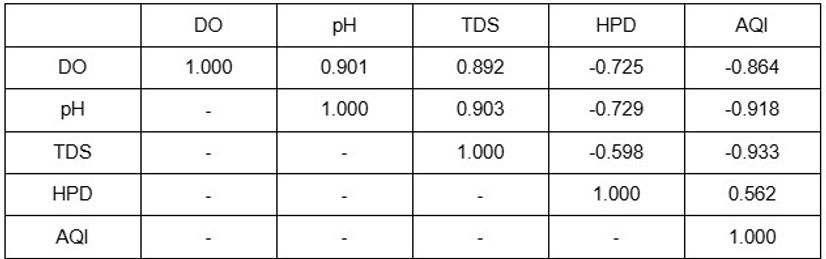
Im Gegensatz zu den vorherigen Korrelationsmatrizen weist die kumulative Tabelle hohe Pearson-Korrelationskoeffizienten zwischen allen Paaren der verwendeten physikochemischen Parameter auf, deren Beträge zwischen 0,691 und 0,896 liegen. Besonders auffällige Parameterpaare mit extrem starken Zusammenhängen sind DO und pH mit einem Koeffizienten von 0,901, DO und TDS mit einem Koeffizienten von 0,8942, pH und AQI mit einer Korrelation von -0,918 sowie AQI und TDS mit einer Korrelation von -0,933. Da jedoch die Beträge aller Koeffizienten über 0,562 liegen, können alle Korrelationen zwischen den Parametern als stark betrachtet werden. Dieser Unterschied in der Stärke der Korrelation im Vergleich zu den vorherigen Korrelationsmatrizen, die die Parameter jedes einzelnen Flusses untersuchten, verdeutlicht, dass die Nullordnungsbeziehungen zwischen Parametern stark erkennbar sind, wenn man die Korrelation auf einer größeren Ebene betrachtet, insbesondere durch die kumulative Beobachtung von Flüssen anstatt durch die detaillierte Untersuchung der Unterschiede zwischen nahegelegenen Erhebungsorten jedes Gewässers.
Die Trends stimmen auch mit der Annahme überein, dass HPD und AQI als Indikatoren für industrielle Verschmutzung dienen und direkt mit den Wasserparametern nahegelegener Flüsse korrelieren. Da DO, pH und TDS einen negativen Pearson-Korrelationskoeffizienten mit den beiden Indikatoren aufwiesen, stehen alle Flussparameter in einem inversen Zusammenhang mit industrieller Verschmutzung: Höhere Werte der Flussparameter deuten auf niedrigere Niveaus industrieller Verschmutzung sowie höhere Wasserqualität hin und umgekehrt. Folglich zeigen alle anderen Parameterpaare positive Zusammenhänge. Da alle Parameter den hohen Verschmutzungsgrad des Han-Flusses im Vergleich zur Donau bestätigten, verdeutlicht die starke Beziehung zwischen allen Parametern, die durch die Pearson-Korrelationsmatrix dargestellt wird, diese Schlussfolgerung als besonders zuverlässig. Diese Schlussfolgerung deckt sich auch mit der Tendenz, dass der Han-Fluss offenbar stärkere industrielle Aktivitäten erlebt als die Donau, was die Industrialisierung als zentrale Variable für die Wasserqualität und den Verschmutzungsgrad der beiden Flüsse nahelegt. Schließlich weist die Korrelationsmatrix alle fünf untersuchten Parameter als geeignet aus, um den Grad industrieller Verschmutzung zwischen verschiedenen Flüssen zu vergleichen.
3.7 Maschinelles Lernen zur Modellierung der erhobenen Daten
Während die Beziehung zwischen den fünf Parametern (DO, pH, TDS, HPD, AQI) identifiziert wurde, bleibt das Ziel der Arbeit, den Menschen eine zugängliche und erschwingliche Methode zur Messung industrieller Verschmutzung zu bieten, bislang unerreicht. DO-, pH- und TDS-Daten können mit kostengünstigen Messgeräten mit akzeptabler Fehlermarge erhoben werden, während HPD regelmäßig von der Regierung mit nahezu perfekter Genauigkeit berechnet wird. Der AQI hingegen ist aufgrund der geringen Zahl an Messstationen in öffentlichen Daten begrenzt verfügbar und erfordert fortschrittliche Geräte, die bis zu mehrere tausend Dollar kosten, um die Luftverschmutzung präzise zu messen. Dies führt dazu, dass Daten mit geringer Genauigkeit erhoben werden oder in manchen Gebieten gar nicht zugänglich sind.
Um dieses Problem zu lösen und gleichzeitig die Möglichkeit der Anwendung der in der Arbeit ermittelten Parameter aufzuzeigen, wurden verschiedene computergestützte Modelle entwickelt, die den AQI basierend auf Daten anderer Parameter schätzen. Da Individuen solche Modelle zur Schätzung des AQI für einen bestimmten Fluss verwenden würden, wurde der Datensatz in die Daten des Han- und der Donau-Fluss aufgeteilt, wobei der erste Datensatz zur Modellschulung und der zweite Datensatz zum Vergleich von Vorhersagen und tatsächlichen Werten genutzt wurde. Da die Studie den AQI und HPD für die Jahre 2023 und 2024 untersuchte, in denen auch die Flussparameter erhoben wurden, wurden die durchschnittlichen AQI- und HPD-Werte als Testdatensatz verwendet. Der in der Bibliothek eingebaute Standard-Scaler wurde genutzt, um die Variablen durch die Modelle zu kalibrieren und auszugleichen.
3.8 Genauigkeit der Modelle
Zusätzlich zu den fünf Basismodellen und den drei Methoden der Merkmalsauswahl/Datenreduzierung, die in der Methodik erwähnt wurden, wurden bis zu zwei Ebenen der Merkmalsauswahl angewandt, um die Modelle zu erstellen. Modelle, in denen vier oder mehr Merkmale ausgewählt wurden, wurden ausgeschlossen, da die Merkmalsauswahl darauf abzielt, die Gesamtzahl der Parameter zur Vorhersage des AQI zu verringern (CAI wurde erneut als AQI-Typ für Vorhersagen gewählt). Aus ähnlichem Grund wurden auch 2-Ebenen-Modelle nicht berücksichtigt, wenn die zweite Ebene die gleiche Anzahl oder mehr Merkmale auswählte als die erste. Da bisher kaum oder gar keine Forschung zur Modellierung dieser Parameter durchgeführt wurde, wurden Kombinationen aus Methoden der Merkmalsauswahl (PCA, RFE, UNI) und Basismodellen/ Klassifikatoren (Linear, SLP, Lasso, Linear SVR, RFR) getestet, was zu insgesamt 185 Modellen führte. Die Ergebnisse aller Modelle sind im Anhang dargestellt. Die Arbeit prüft verschiedene computergestützte Modelle, wobei Root Mean Squared Error (RMSE) und Mean Absolute Error (MAE) zwischen den vorhergesagten Werten und den tatsächlichen AQI-Werten zur Bewertung der Genauigkeit verwendet werden. Die durchschnittlichen, maximalen, minimalen und zweikleinsten RMSEs sowie MAEs der getesteten Modelle sind in den Tabellen 19 und 20 dargestellt.
Tabelle 19. Durchschnittlicher, minimaler und maximaler RMSE der getesteten Modelle

Tabelle 20. Mittlerer, minimaler und maximaler MAE der getesteten Modelle

Im Allgemeinen waren die RMSE- und MAE-Werte aller Modelle recht hoch. Der RMSE schwankte erheblich zwischen 30,324 (Lasso-Regression) und 79,902 (Linear-PCA3-RFE2- und Linear-PCA3-UNI2-Modelle); der MAE bewegte sich in einem ähnlichen Bereich zwischen 26,014 (Lasso-Regression) und 78,433 (Linear-PCA3-RFE2- und Linear-PCA3-UNI2-Modelle). Basierend auf beiden Fehlern scheint das Lasso-Regression-Modell ohne zusätzliche Merkmalsauswahlebenen das genaueste zu sein. Der RMSE der Vorhersagen mit Lasso-Regression betrug 30,324, etwas geringer als der der linearen Regression mit 30,542. Ebenso lag der MAE mit 26,014 nahe am Wert der linearen Regression von 26,206. Der MAE der Lasso-Regression entsprach 61 % des durchschnittlichen MAE von 49,806 und der RMSE 53 % des durchschnittlichen RMSE von 49,131, was die signifikante Genauigkeit dieses Verfahrens im Vergleich zu anderen Modellen zeigt. Daher, obwohl die Modelle ungenau und wenig bedeutsam für die Schätzung des AQI anhand der vier Parameter erscheinen, kann das SVR-PCA2-RFE1-Modell als akzeptabel genau für AQI-Vorhersagen angesehen werden. Durch dieses Modell wird es möglich sein, das Ausmaß industrieller Verschmutzung in einem Gebiet kostengünstig zu überprüfen, was das Bewusstsein für die Auswirkungen industrieller Verschmutzung schärfen und letztlich Menschen motivieren kann, sich gegen diese Zerstörung der Umwelt einzusetzen.
3.9 Ursachen für ungenaue Vorhersagen
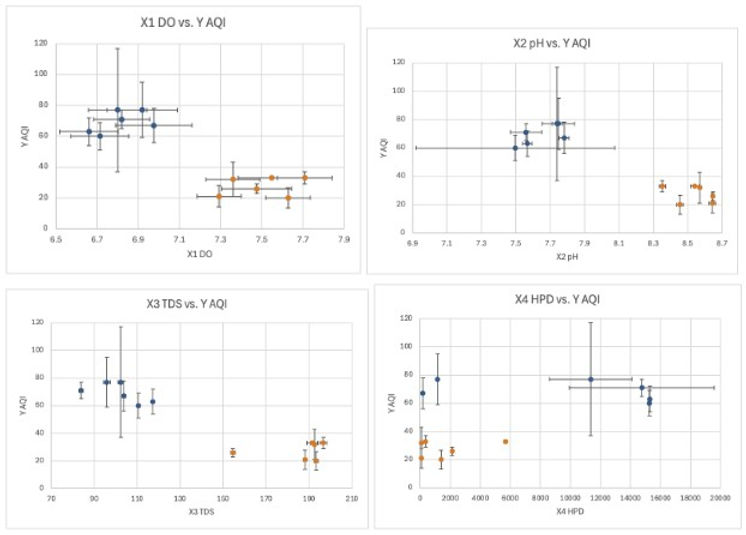
Die großen Fehler in den Vorhersagen der Modelle waren aufgrund einer Reihe von Einschränkungen hinsichtlich der Parameter und Daten zu erwarten. Erstens ist der AQI selbst ein sehr volatiler Parameter, da ihn eine Vielzahl schnell wechselnder, unkontrollierter Variablen beeinflusst, wie etwa Windstärke, Ausstoßrate von Schadstoffen oder Wetterlage. In Verbindung mit der begrenzten Anzahl an AQI-Messstationen und verfügbaren Daten erschwert diese Ungenauigkeit des Datensatzes die Vorhersage des AQI. Ein weiterer möglicher Grund ist die geringe Anzahl an Datenerhebungsorten selbst, da 12 Standorte nur 6 Datenpunkte für das Training und 6 für das Testen des Modells ergaben, was eine extrem kleine Menge darstellt. Ebenso schränkte die begrenzte Anzahl von Parametern vermutlich die Anzahl der Muster ein, die das Modell identifizieren konnte, was seine Ungenauigkeit erhöhte. Der einflussreichste Faktor, der die Ungenauigkeit der Modelle verursacht, ist jedoch vermutlich die Clusterung der Daten nach Flüssen, da die Arbeit bereits festgestellt hat, dass die Flussdaten gruppiert sind und daher Daten von mehr Flüssen (die nach derselben Methodik erhoben wurden) erforderlich sind, um die allgemeine Beziehung zwischen Parametern und industrieller Verschmutzung in Flüssen präzise modellieren zu können. Da die Daten geclustert sind, werden Datensätze von mehr als einem Fluss benötigt, um eine halbwegs genaue Regression zu bilden, die die Trends über die einzelnen Flüsse hinweg identifiziert, anstatt spezifisch für nur einen Fluss zu sein. Diese wesentliche Einschränkung kann durch einen Machine-Learning-Ansatz gelöst werden, bei dem Online-Datenbanken in die computergestützten Modelle integriert werden, was deren Genauigkeit erheblich steigern würde. Die Clusterung wird in den unten dargestellten Streudiagrammen in Abbildungen 4 bis 7 veranschaulicht, wobei die Diagramme links auf Daten des Han-Flusses basieren und die Diagramme rechts auf Daten der Donau.
Abbildungen 4-7. Streudiagramme jedes Parameters gegen den AQI, die die Clusterung der Daten zeigen (Datensatz Han-Fluss in Blau, Datensatz Donau in Orange)
3.10 Analyse der Möglichkeit zur Verbesserung des Modells
Um zu prüfen, ob eine erhöhte Anzahl von Flüssen im Datensatz die Möglichkeit bietet, die Vorhersagen der AQIs durch das Modell zu verbessern, muss die Clusterbildung in der Analyse des Modells vorhanden sein, sodass das Modell eine Regression erstellen kann, die durch jedes Cluster verläuft. Während es ideal wäre, die Clusterung der Daten für jedes Modell zu analysieren, würde die Erstellung und Untersuchung von Streudiagrammen für 185 Kombinationen von Modellen und Merkmalsauswahlen die Studie erheblich verlängern und verkomplizieren. Daher wurden die Streudiagramme der Daten nach Normalisierung und Anwendung der PCA-Merkmalsauswahl für die Analyse ausgewählt, da solche Streudiagramme für die Visualisierung geeignet sind. Das Streudiagramm der ursprünglichen Daten wird unten zusammen mit dem der normalisierten Daten in den Abbildungen 8-9 dargestellt.
Abbildungen 8-9. Streudiagramme der ursprünglichen und normalisierten Daten
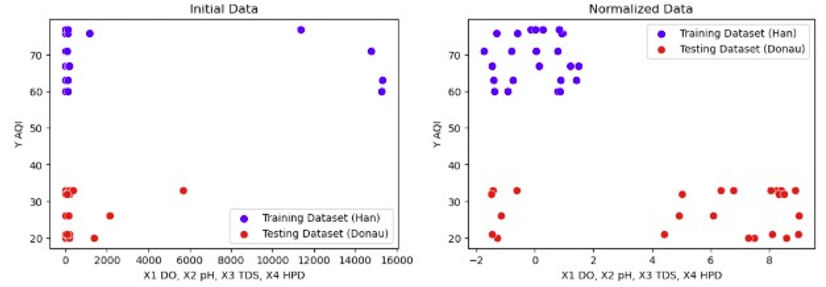
As demonstrated by the clear difference between the two figures above, the clustering of the data from the Han and Donau river appears more evident: while four outliers from the training dataset (Han river) dataset were initially located in the upper right-hand corner, the outliers became part of the cluster after normalizing the data. Contrastingly, new outliers appeared among the testing dataset (Donau river) although of a less extreme degree than the previous outliers, suggesting the limitations of clustering of data with only normalization. For a more detailed analysis of the outliers, scatterplots labelled with specific parameters are provided in figures 10-11.
Figures 10-11. Labelled scatterplots of initial and normalized data
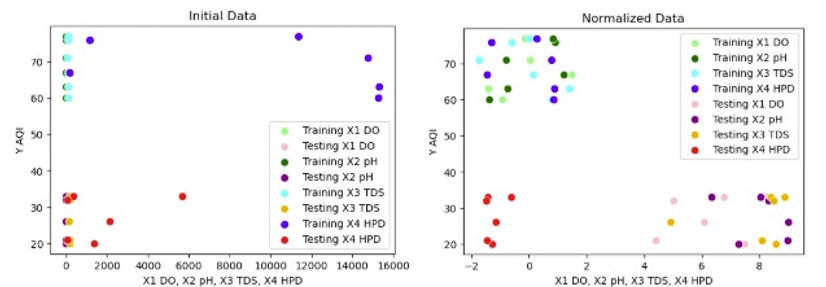
Wie in den Streudiagrammen zu erkennen ist, waren die Ausreißer beider Flüsse auf HPD-Daten beider Flüsse zurückzuführen. Diese Beobachtung legt nahe, dass Modelle mit größeren Datensätzen den AQI relativ genau vorhersagen können, wenn Merkmalsauswahlebenen angewendet und HPD-Daten effektiv entfernt werden. Dies basiert jedoch auf der Annahme, dass die HPD-Daten aller Flüsse den Gesamttrend des Datensatzes im Vergleich zu DO, pH und HPD nicht ergänzen, was mit Daten von nur zwei Flüssen nicht gerechtfertigt werden kann. Anschließend wurden die Streudiagramme nach Anwendung der PCA analysiert, um zu untersuchen, ob HPD-Daten aus dem Test- und Trainingsdatensatz entfernt wurden.
Abbildungen 12–14. Streudiagramme normalisierter Daten nach Anwendung der PCA

Nachdem PCA angewendet wurde, bestätigte sich die Annahme, dass HPD aus dem Datensatz entfernt wurde, was die Möglichkeit weiter untermauert, dass das Machine-Learning-Modell AQI mit größeren Datensätzen genauer vorhersagen kann. Vergleicht man das Streudiagramm der normalisierten Daten, so wurden die Ausreißer nach Anwendung von PCA mit 3, 2 und 1 Komponenten entfernt. Die Clusterung ist bei PCA2 am deutlichsten erkennbar, was zu der Prognose führt, dass die Auswahl von zwei Merkmalen das genaueste Modell liefern würde, sobald mehr Daten hinzugefügt werden.
3.11 Modell mit erweitertem Datensatz
Nachdem festgestellt wurde, dass die Ungenauigkeit des Modells wahrscheinlich auf die Clusterung der Daten zurückzuführen ist, wurden öffentliche Daten genutzt, um den Datensatz der Flüsse zu erweitern, mit denen das Modell trainiert und getestet werden konnte [16-19]. Zwei verschiedene Datensätze wurden getestet: 2015-2024 und 2019-2024, jeweils mit 65 bzw. 44 Flüssen aus verschiedenen Ländern der Welt. Zusätzlich wurden, da die Gesamtbevölkerung bei den Tests eine Korrelation mit den Vorhersagen zu zeigen schien, weitere Datensätze mit der Bevölkerung als Variable X5 verwendet. Unter Verwendung der Mittelwerte und der Annahme, dass jeder Fluss einen Datenpunkt darstellt, wurde der Datensatz mit den Modellen gemischt, um die Zuverlässigkeit des Modells zu prüfen, indem die große Menge an Daten, die es für Training und Tests verwendet, randomisiert wurde. Alle oben diskutierten Modelle (Regressoren und Klassifikatoren) wurden verwendet, und Techniken der Dimensionsreduktion wurden von Methoden der Merkmalsauswahl unterschieden und als letzte Schicht des Modells angewendet, um Genauigkeit zu gewährleisten, indem zunächst mit der Merkmalsauswahl Rauschen reduziert wurde, bevor mit der Dimensionsreduktion die Interpretierbarkeit verändert wurde. Dieses Verfahren erlaubte es, 11.632 verschiedene Permutationen zu testen, die sich für alle Datensätze zusammen auf über 45.000 summierten. RFE wurde nicht auf NuSVR, Epsilon SVR, BR oder HGBR angewendet, da solche Regressoren keine automatische Rangordnung von Merkmalen erstellen, was zur Implementierung von RFE erforderlich ist. Zudem wurde K-Fold-Cross-Validation eingesetzt, um die Genauigkeit des Modells zu erhöhen, und für jede Permutation wurden 5 Folds durchgeführt. Da die Daten randomisiert wurden, wurden fünf Durchläufe durchgeführt, um die Genauigkeit zu bestätigen. Die Ergebnisse der minimalen Fehler sind in den Tabellen 21 bis 32 dargestellt.
Tabellen 21-24. Mittelwert und Standardabweichung von RMSE und MAE der linearen Modelle 2015-2024 und 2019-2024

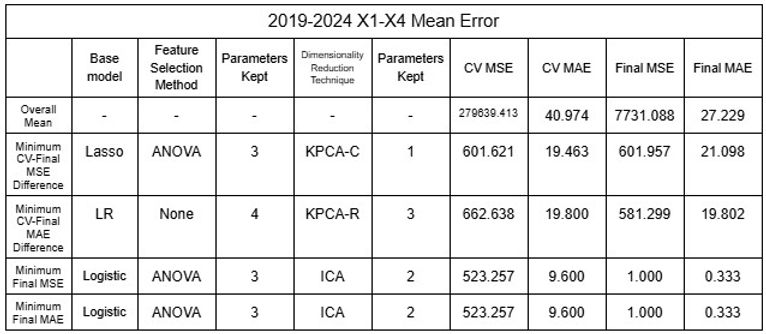

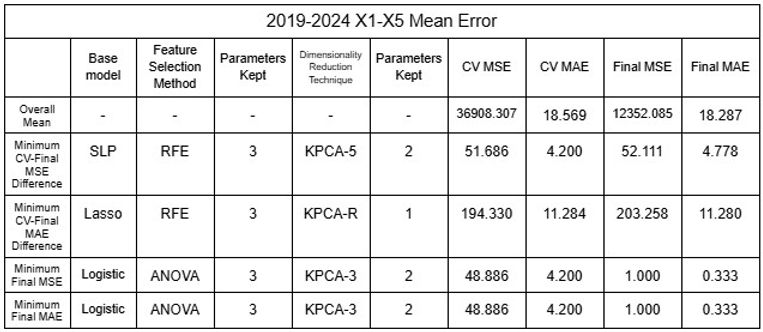
Tabellen 25–28. Mittelwert und Standardabweichung RMSE und MAE der SVR-Modelle 2015–2024 und 2019–2024
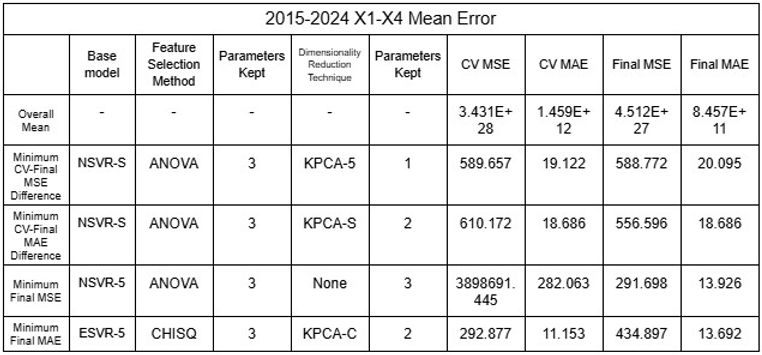

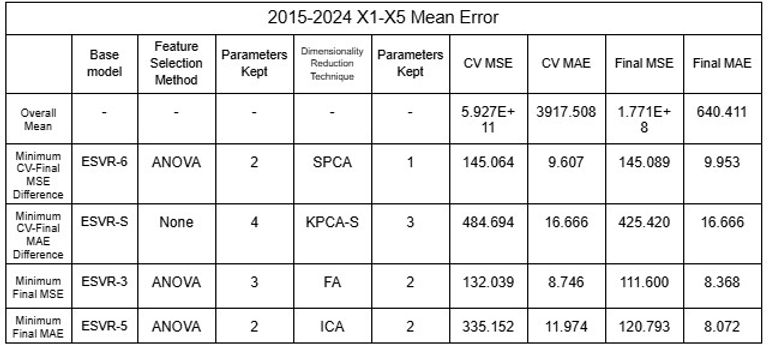
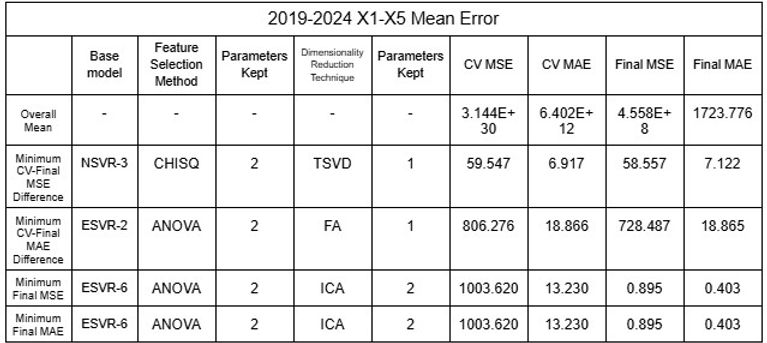
Tabellen 29-32. Mittelwert und Standardabweichung RMSE und MAE der Modellensembles 2015-2024 und 2019-2024

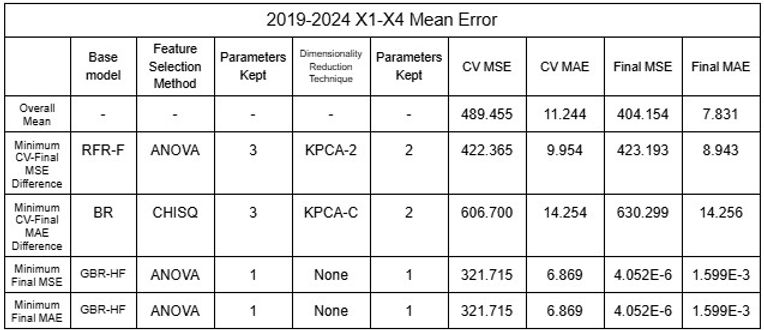


Die niedrigen Mittelwerte der Fehler deuten eindeutig darauf hin, dass die Modelle mit den großen Datensätzen ein erhebliches Maß an Genauigkeit aufwiesen. Darüber hinaus veranschaulichen NSVR-3 mit CHISQ2 und TSVD1 oder RFR-F mit RFE2 und KPCA1-6 Modelle mit minimalem Unterschied zwischen durchschnittlichem Cross-Validation-Fehler und endgültigem Fehler nach dem Testen, was zeigt, dass die Modelle nicht überangepasst wurden und zuverlässig sind. Während nichtlineare SVRs mit einem minimalen MSE und MAE von 0,895 bzw. 0,403 die genauesten zu sein scheinen, können die oben genannten unterschiedlichen Modelle je nach Ziel des Nutzers ausgewählt werden, etwa zur Minimierung der Differenz zwischen CV- und Final-Fehler oder zur Priorisierung von MAE gegenüber MSE.
4. Einschränkungen
4.1 Einschränkungen der Datenerhebung
Eine bemerkenswerte Einschränkung der Fallstudie ist die erhebliche Variation zwischen den Datenpunkten. Die Schwankungen in den Umweltvariablen, wie der Probentemperatur, waren in situ aufgrund der volatilen Bedingungen am Standort ausgeprägter. Im Gegensatz dazu wiesen die physikalischen Daten zum gelösten Sauerstoff erhebliche Abweichungen im Vergleich zu den pH- und TDS-Daten auf, vermutlich weil die Daten ex-situ erhoben wurden. Darüber hinaus führten die unterschiedlichen Erhebungsorte im Mittellauf in den Jahren 2023 und 2024, obwohl sie die Distanz zwischen den Standorten bis zu einem gewissen Grad berücksichtigten, zu Abweichungen bei den Bevölkerungsdichtewerten für diesen Abschnitt.
4.2 Einschränkungen der Datenmodellierung
Das Ergebnis, dass die Merkmalsauswahl die Genauigkeit der Machine-Learning-Modelle erhöht, steht im Widerspruch dazu, dass das genaueste mit Han- und Donau-Fluss trainierte Modell die Lasso-Regression war, die mit normalisierten Daten ohne Merkmalsauswahlebenen trainiert wurde. Dieser Gegenbefund lässt sich jedoch leicht entkräften, da alle Modelle hohe Fehlerraten aufwiesen und auch das ausgewählte Modell dennoch ungenau ist.
5. Fazit
Ziel dieser Studie war die Untersuchung der industriellen Verschmutzung des Han-Flusses in Südkorea und der Donau in Österreich. Dabei wurden Daten zu DO, pH-Wert und TDS als Parameter des Oberflächenwassers der Flüsse erhoben. Die Studie korrelierte zudem verschiedene Parameter, um Zusammenhänge zu untersuchen und zuverlässige Indikatoren zu identifizieren. Dabei wurden die physisch erhobenen Daten mithilfe der Pearson-Korrelationskoeffizientenmatrizen mit öffentlichen Daten zu HPD und AQI als zusätzlichen Parametern verknüpft. Eine qualitative Bewertung des Schweregrads der industriellen Verschmutzung in beiden Flüssen erfolgte ebenfalls anhand von Variablen wie der Menge der in die Flüsse eingeleiteten Fabrikabwässer oder den Folgen der Urbanisierung. Dies verdeutlichte das erhebliche Ausmaß der industriellen Verschmutzung in Südkorea, die den Han-Fluss im Vergleich zu Österreich und der Donau betrifft. Die Daten zu den Flussparametern, HPD und AQI stimmten mit den allgemeinen Trends überein, dass der Han-Fluss deutlich stärker verschmutzt ist als die Donau. Die Datenstandorte zeigten vergleichsweise hohe DO- und TDS-Werte, niedrige pH-Werte, hohe HPD-Werte und hohe AQI-Werte (CAI als AQI-Typ), was mit der qualitativen Bewertung übereinstimmt. Die Korrelationsmatrizen zeigten asymmetrische Muster, wenn Parameter von Datenstandorten innerhalb des Flusses verglichen wurden. Beim kumulativen Vergleich zeigten jedoch alle Parameterpaare starke Beziehungen nullter Ordnung mit der Größe des Pearson-Koeffizienten zwischen 0,691 und 0,903. Die Ergebnisse zeigen die Wechselwirkung zwischen den fünf untersuchten Parametern und ihre Eignung als Indikatoren für industrielle Verschmutzung beim Vergleich mehrerer Flüsse. Die auf der Grundlage der zwischen den Parametern ermittelten Beziehungen erstellten Datenanalysemodelle ermöglichen Vorhersagen von AQI-Daten mit unterschiedlicher Genauigkeit. Diese Fähigkeit zur AQI-Vorhersage macht teure Messgeräte zur Bestimmung des Ausmaßes der industriellen Verschmutzung überflüssig, ermöglicht es der breiten Öffentlichkeit, auf solche Daten zuzugreifen oder sie zu erhalten, und schärft das Bewusstsein für das globale Problem des Klimawandels. In ähnlicher Weise können andere Forscher diese Modelle nutzen, um den AQI basierend auf anderen miteinander verbundenen Parametern zu schätzen und so ihren Forschungsbereich zu erweitern. Die Studie bestätigt, dass der Han-Fluss einer schweren industriellen Verschmutzung ausgesetzt ist, während die Donau nur in einem tolerierbaren Maß verunreinigt ist. Dies wird durch die gesammelten Daten zu physikochemischen Parametern des Oberflächenwassers des Flusses, die HPD- und AQI-Werte der Datenstandorte sowie die Vielzahl der Faktoren, die die industrielle Verschmutzung des Flusses beeinflussen, gestützt. Die Studie legt außerdem fest, dass Lasso-Regressionsmodelle zur Vorhersage des AQI als AQI mit einigen Fehlern geeignet sind, wobei RMSE und MAE vergleichsweise niedrige Werte von 30,324 bzw. 26,014 aufweisen. In naher Zukunft ist auch die Implementierung eines maschinellen Lernansatzes unter Verwendung von Datendatenbanken möglich, wodurch die Genauigkeit verbessert und möglicherweise andere Modelle vorgeschlagen werden, die besser für Vorhersagen geeignet sind. Schließlich scheint ESVR-6 unter Anwendung von ANOVA2 und ICA2 mit endgültigen MSE- und MAE-Werten von 0,895 und 0,403 das genaueste Modell zu sein. Da jedoch bei Modellen wie NSVR-3 mit CHISQ2 und TSVD1 oder RFR-F mit RFE2 und KPCA1-6 die Unterschiede zwischen der durchschnittlichen Kreuzvalidierung und dem endgültigen Fehler geringer sind, können für unterschiedliche Zwecke unterschiedliche Modelle ausgewählt werden, wobei die Mehrheit der Modelle dennoch eine hohe Genauigkeit in allen Kategorien gewährleistet.
6. Danksagung
Diese Forschung wurde individuell durchgeführt, aber ich möchte Leon Plakolm als meinem Forschungsmentor danken, der den Prozess der Veröffentlichung dieses Artikels überwacht hat.
7. Datenverfügbarkeit
Daten werden auf Anfrage zur Verfügung gestellt. Ebenso kann Code zum Testen von Modellen angefordert werden.
8. Referenzen
Acar, S., & Mahmut Tekce. (2014). Economic Development and Industrial Pollution in the Mediterranean Region: A Panel Data Analysis. Retrieved December 9, 2024, from Loyola eCommons website: https://ecommons.luc.edu/meea/190/
AirKorea: Introduction to the AQI. (2022). Retrieved December 10, 2024, from Airkorea.or.kr website: https://www.airkorea.or.kr/eng/khaiInfo?pMENU_NO=166
An, I. (2022, September 15). Breaking News/ 11 Million Tons of Polluted Sewage Discharged into Han River Basin/Day, “Pollution of Drinking Water Sources Worsened.” Retrieved December 16, 2024, from Egreen News website: https://m.egreen-news.com/11480
Anderson, E. P., Jackson, S., Tharme, R. E., Douglas, M., Flotemersch, J. E., Zwarteveen, M., … Roux, D. J. (2019). Understanding rivers and their social relations: A critical step to advance environmental water management. WIREs Water, 6(6). https://doi.org/10.1002/wat2.1381
Andrej Dávid, & Madudová, E. (2019). The Danube river and its importance on the Danube countries in cargo transport. Transportation Research Procedia, 40, 1010–1016. https://doi.org/10.1016/j.trpro.2019.07.141
Anh, N. T., Can, L. D., Nhan, N. T., Schmalz, B., & Luu, T. L. (2023). Influences of key factors on river water quality in urban and rural areas: A review. Case Studies in Chemical and Environmental Engineering, 8, 100424. https://doi.org/10.1016/j.cscee.2023.100424
Arief Dhany Sutadian, Nitin Muttil, Yilmaz, A. G., & Perera, C. (2015). Development of river water quality indices—a review. Environmental Monitoring and Assessment, 188(1). https://doi.org/10.1007/s10661-015-5050-0
Bashir, I., Lone, F. A., Bhat, R. A., Mir, S. A., Dar, Z. A., & Dar, S. A. (2020). Concerns and Threats of Contamination on Aquatic Ecosystems. Springer EBooks, 1–26. https://doi.org/10.1007/978-3-030-35691-0_1
Bhuyan, M. S., & Islam, M. S. (2017). Status and Impacts of Industrial Pollution on the Karnafully River in Bangladesh: A Review. International Journal of Marine Science. https://doi.org/10.5376/ijms.2017.07.0016
Blanchet, S., Prunier, J. G., Paz‐Vinas, I., Keoni Saint‐Pé, Rey, O., Raffard, A., … Dubut, V. (2020). A river runs through it: The causes, consequences, and management of intraspecific diversity in river networks. Evolutionary Applications, 13(6), 1195–1213. https://doi.org/10.1111/eva.12941
Cho, C. (2023, June 15). The Han River has the 43rd highest contamination density in the world. Retrieved December 16, 2024, from The Herald Insight website: http://www.heraldinsight.co.kr/news/articleView.html?idxno=3205#:~:text=According%20to%20research%2C%20the%20Han,filtered%20by%20wastewater%20treatment%20plants.
Die Donaustadt in Zahlen - Statistiken zum 22. Bezirk. (2020, December 15). Retrieved December 10, 2024, from Wien.gv.at website: https://www.wien.gv.at/statistik/bezirke/donaustadt.html
Die Leopoldstadt in Zahlen - Statistiken zum 2. Bezirk. (2020, December 14). Retrieved December 10, 2024, from Wien.gv.at website: https://www.wien.gv.at/statistik/bezirke/leopoldstadt.html
Ein Blick auf die Gemeinde Korneuburg: 1.1 Fläche und Flächennutzung. (2024, January 1). Retrieved December 10, 2024, from Statistik.at website: https://www.statistik.at/blickgem/G0101/g31213.pdf
Gasparotti, C. M. (2014). The main factors of water pollution in Danube River basin. Euro Economica, 33(01), 91–106. Retrieved from https://www.ceeol.com/search/article-detail?id=284478
Google Maps. (2019). Google Maps. Retrieved December 16, 2024, from Google Maps website: https://www.google.com/maps
Gunkel, G., Kosmol, J., Sobral, M., Rohn, H., Montenegro, S., & Aureliano, J. (2006). Sugar Cane Industry as a Source of Water Pollution – Case Study on the Situation in Ipojuca River, Pernambuco, Brazil. Water Air & Soil Pollution, 180(1-4), 261–269. https://doi.org/10.1007/s11270-006-9268-x
Hanam Province Official E-Government Website. (2023). Neighborhood News - Administrative Welfare Center. Retrieved December 11, 2024, from Hanam.go.kr website: https://www.hanam.go.kr/jumin/contents.do?key=11326
Helmut Habersack, Hein, T., Stanica, A., Liska, I., Mair, R., Jäger, E., … Bradley, C. (2015). Challenges of river basin management: Current status of, and prospects for, the River Danube from a river engineering perspective. The Science of the Total Environment, 543, 828–845. https://doi.org/10.1016/j.scitotenv.2015.10.123
Hwang, J. H., Park, S. H., & Song, C. M. (2020). A Study on an Integrated Water Quantity and Water Quality Evaluation Method for the Implementation of Integrated Water Resource Management Policies in the Republic of Korea. Water, 12(9), 2346–2346. https://doi.org/10.3390/w12092346
International Commission for the Protection of the Danube River. (2021). Water Quality. Retrieved December 16, 2024, from Icpdr.org website: https://www.icpdr.org/tasks-topics/topics/water-quality
International Commission for the Protection of the Danube River. (2022, June 9). Annual Bathing Water Report Published: Danube Countries at Top of Ranking | ICPDR - International Commission for the Protection of the Danube River. Retrieved December 16, 2024, from Icpdr.org website: https://www.icpdr.org/tasks-topics/topics/water-quality/annual-bathing-water-report-published-danube-countries-top
Jung, D. (2019, October 28). Han river water pollution, highest accident rate among the four major rivers. Retrieved December 16, 2024, from Oh My News website: https://www.ohmynews.com/NWS_Web/View/at_pg.aspx?CNTN_CD=A0002582171
Kim, H.-K., & Seoul National University Graduate School of Environmental Studies. (2024). The Modern Evolution of Environmentalism : The Case of Korea, 1960~1989. Journal of Environmental Studies, 28, 30–41. https://hdl.handle.net/10371/90500
Kondolf G. Mathias, & Pinto, P. J. (2016). The social connectivity of urban rivers. Geomorphology, 277, 182–196. https://doi.org/10.1016/j.geomorph.2016.09.028
Lee, S. D., Yun, S. M., Cho, P. Y., Yang, H.-W., & Kim, O. J. (2019). Newly Recorded Species of Diatoms in the Source of Han and Nakdong Rivers, South Korea. Phytotaxa, 403(3), 143–143. https://doi.org/10.11646/phytotaxa.403.3.1
Lin, L., Yang, H., & Xu, X. (2022). Effects of Water Pollution on Human Health and Disease Heterogeneity: A Review. Frontiers in Environmental Science, 10. https://doi.org/10.3389/fenvs.2022.880246
Ministry of the Interior and Safety of South Korea. (2015). Resident Registration Population Statistics Ministry of the Interior and Safety. Retrieved December 11, 2024, from Mois.go.kr website: https://jumin.mois.go.kr/
Mishra, R. K., Mentha, S. S., Misra, Y., & Dwivedi, N. (2023). Emerging pollutants of severe environmental concern in water and wastewater: A comprehensive review on current developments and future research. Water-Energy Nexus, 6, 74–95. https://doi.org/10.1016/j.wen.2023.08.002
Mohamed, A. (2024). Water Pollution: Causes, Impacts, and Solutions: a critical review. (76), 1–18. https://doi.org/10.37376/jsh.vi76.5785
Namyangju Province Official E-Government Website. (2024). General information - Introduction - Wabu-eup - Administrative welfare center/town/village - Namyangju introduction - Namyangju City Hall. Retrieved December 11, 2024, from Namyangju City Hall website: https://www.nyj.go.kr/www/contents.do?key=2569
Olías, M., Cerón, J. C., Moral, F., & Ruiz, F. (2006). Water quality of the Guadiamar River after the Aznalcóllar spill (SW Spain). Chemosphere, 62(2), 213–225. https://doi.org/10.1016/j.chemosphere.2005.05.015
P.U Igwe, C.C Chukwudi, F.C Ifenatuorah, I.F Fagbeja, & C.A Okeke. (2017). A Review of Environmental Effects of Surface Water Pollution. Ijaers.com, 4(12). Retrieved from https://ijaers.com/detail/a-review-of-environmental-effects-of-surface-water-pollution/
Radu, V.-M., Ionescu, P., Deak, G., Diacu, E., Ivanov, A. A., Zamfir, S., & Marcus, M.-I. (2020). Overall assessment of surface water quality in the Lower Danube River. Environmental Monitoring and Assessment, 192(2). https://doi.org/10.1007/s10661-020-8086-8
Reinartz, R., Lippold, S., D. Lieckfeldt, & Ludwig, A. (2011). Population genetic analyses of Acipenser ruthenus as a prerequisite for the conservation of the uppermost Danube population. Journal of Applied Ichthyology, 27(2), 477–483. https://doi.org/10.1111/j.1439-0426.2011.01693.x
Research Report - Research on the establishment of a conservation plan for the Han River Estuary Wetland Protection Area (20-24). (2019, October 7). Retrieved December 16, 2024, from Ecopi.co.kr website: http://ecopi.co.kr/index.php?mid=board_NtgR13&document_srl=79524
Roy, M., & Shamim, F. (2020). Research on the Impact of Industrial Pollution on River Ganga: A Review. International Journal of Prevention and Control of Industrial Pollution, 6(1), 43–51. Retrieved from https://chemical.journalspub.info/index.php?journal=JPCIP&page=article&op=view&path%5B%5D=961
Rusydi, A. F. (2018). Correlation between conductivity and total dissolved solid in various type of water: A review. IOP Conference Series: Earth and Environmental Science, 118(1), 012019. https://doi.org/10.1088/1755-1315/118/1/012019
Schmid, M., Haidvogl, G., Friedrich, T., Funk, A., Schmalfuss, L., Schmidt-Kloiber, A., & Hein, T. (2023). The Danube: On the Environmental History, Present, and Future of a Great European River. UNESCO EBooks, 637–671. https://doi.org/10.54677/intf8577
Seoul Statistical Integration Platform. (2019). Administrative District Population Statistical Table. Retrieved December 11, 2024, from Eseoul.go.kr website: https://stat.eseoul.go.kr/statHtml/statHtml.do?orgId=201&tblId=DT_201004_O010001&conn_path=I2&obj_var_id=&up_itm_id=
Shin, H.-J., Kim, H., Jeon, C.-H., Jo, M.-W., Nguyen, T., & Tenhunen, J. (2016). Benefit Transfer for Water Management along the Han River in South Korea Using Meta-Regression Analysis. Water, 8(11), 492–492. https://doi.org/10.3390/w8110492
Shin, M.-S., Lee, J.-Y., Kim, B.-C., & Bae, Y.-J. (2011). Long-term variations in water quality in the lower Han River. Journal of Ecology and Field Biology, 34(1), 31–37. https://doi.org/10.5141/jefb.2011.005
Stagl, J., & Hattermann, F. (2015). Impacts of Climate Change on the Hydrological Regime of the Danube River and Its Tributaries Using an Ensemble of Climate Scenarios. Water, 7(11), 6139–6172. https://doi.org/10.3390/w7116139
Statistik Austria. (2024a, January 1). Ein Blick auf die Gemeinde Haslau-Maria Ellend: 1.1 Fläche und Flächennutzung Q. Retrieved December 10, 2024, from Statistik.at website: https://www.statistik.at/blickgem/G0101/g30711.pdf
Statistik Austria. (2024b, January 1). Ein Blick auf die Gemeinde Klosterneuburg: 1.1 Fläche und Flächennutzung Q. Retrieved December 10, 2024, from Statistik.at website: https://www.statistik.at/blickgem/G0101/g32144.pdf
Statistik Austria. (2024c, January 1). Ein Blick auf die Gemeinde Orth an der Donau: 1.1 Fläche und Flächennutzung Q. Retrieved December 10, 2024, from Statistik.at website: https://www.statistik.at/blickgem/G0101/g30844.pdf
Tahershamsi, A., Bakhtiary, A., & Mousavi, A. (2009). Effects of seasonal climate change on Chemical Oxygen Demand (COD) concentration in the Anzali Wetland (Iran). In 18 th World IMACS / MODSIM. Retrieved from https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=e2ad0665600300db2830f048ad9febc501518e24
Vynokurova, S., Yakovliev, M., Voloshkevich, O., Haidash, O., & Demchenko, V. (2023). Biodiversity assessment of the Danube region as a tool for the development of protected areas in the region. IOP Conference Series: Earth and Environmental Science, 1254(1), 012015. https://doi.org/10.1088/1755-1315/1254/1/012015
World Air Quality Index. (2008). Retrieved December 9, 2024, from aqicn.org website: https://aqicn.org/
Wu, Y., Zhang, L., Wang, J., & Mou, Y. (2021). Communicating Air Quality Index Information: Effects of Different Styles on Individuals’ Risk Perception and Precaution Intention. International Journal of Environmental Research and Public Health, 18(19), 10542–10542. https://doi.org/10.3390/ijerph181910542
Zhang, Z. M., Wang, X. Y., Zhang, Y., Nan, Z., & Shen, B. G. (2012). The Over Polluted Water Quality Assessment of Weihe River Based on Kernel Density Estimation. Procedia Environmental Sciences, 13, 1271–1282. https://doi.org/10.1016/j.proenv.2012.01.120
Buitinck, L., Louppe, G., Blondel, M., Pedregosa, Fabian, Mueller, A., Grisel, O., … Ga"el Varoquaux. (2013). API design for machine learning software: experiences from the scikit-learn project. In ECML PKDD Workshop: Languages for Data Mining and Machine Learning (pp. 108–122).
Cairncross, E. K., John, J., & Zunckel, M. (2007). A novel air pollution index based on the relative risk of daily mortality associated with short-term exposure to common air pollutants. Atmospheric Environment, 41(38), 8442–8454. https://doi.org/10.1016/j.atmosenv.2007.07.003
United Nations Environment Programme. (2024, January 9). GEMStat - The global freshwater quality database. GEMStat. https://gemstat.org/
International Database. (2025). Census.gov; United States Census Bureau. https://www.census.gov/data-tools/demo/idb/#/dashboard?dashboard_page=country&COUNTRY_YR_ANIM=2025&CCODE_SINGLE=UY&subnat_map_admin=ADM1&CCODE=UY
UNdata. (2024). Un.org; United Nations. https://data.un.org/
Air quality database 2022. (2022). Who.int; World Health Organization. https://www.who.int/data/gho/data/themes/air-pollution/who-air-quality-database/2022
Über Mich
Jiwoo Jung ist ein südkoreanischer Schüler der American International School of Vienna. Er ist gerade dabei, sein Programm zur Vorhersage industrieller Umweltverschmutzung patentieren zu lassen und seine Forschungsarbeit zu veröffentlichen. Er plant, Umweltwissenschaften zu studieren.